Giải SBT Toán 11 (Chân trời sáng tạo) Bài tập cuối chương 5 trang 160

Sách bài tập Toán 11 Bài tập cuối chương 5 trang 160

A. TRẮC NGHIỆM

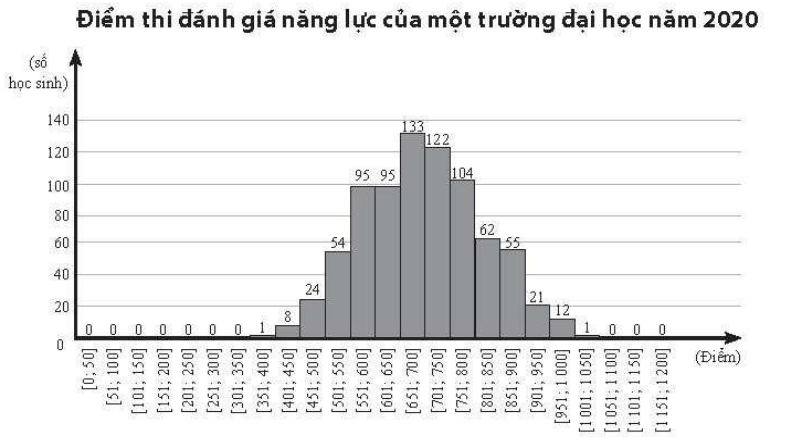
Trả lời các câu hỏi 1 - 5 dựa trên đồ thị thể hiện điểm thi đánh giá năng lực của một trường đại học vào năm 2020 dưới đây.

Câu 1 trang 160 SBT Toán 11 Tập 1: Tổng số học sinh tham gia kì thi đánh giá năng lực trên là

A. 780.

B. 787.

C. 696.

D. 697.

Lời giải:

Đáp án đúng là: B

Tổng số học sinh tham gia kì thi đánh giá năng lực trên là

1 + 8 + 24 + 54 + 95 + 95 + 133 + 122 +104 + 62 + 55 + 21 + 12 + 1 = 787 (học sinh).

Câu 2 trang 160 SBT Toán 11 Tập 1: Giá trị đại diện cho nhóm chứa mốt của mẫu số liệu ghép nhóm trên là

A. 625,5.

B. 675,5.

C. 725,5.

D. 775,5.

Lời giải:

Đáp án đúng là: B

Từ đồ thị và do số học sinh là số nguyên nên ta hiệu chỉnh lại bảng số liệu như sau:

Nhóm chứa mốt của mẫu số liệu ghép nhóm trên là nhóm [650,5; 700,5).

Giá trị đại diện cho nhóm đó là $\frac{1}{2}$(650,5 + 700,5) = 675,5.

Câu 3 trang 160 SBT Toán 11 Tập 1: Giá trị đại diện cho nhóm chứa trung vị của mẫu số liệu ghép nhóm trên là

A. 625,5.

B. 675,5.

C. 725,5.

D. 775,5.

Lời giải:

Đáp án đúng là: B

Gọi x₁; x₂; x₃;...; x₇₈₇ là mẫu số liệu được xếp theo thứ tự không giảm.

Cỡ mẫu n = 787 là số lẻ nên trung vị của mẫu số liệu là: M_e = x₃₉₄. Do x₃₉₄ thuộc nhóm [650,5; 700,5) nên giá trị đại diện cho nhóm đó là: $\frac{1}{2}$(650,5 + 700,5) = 675,5.

Câu 4 trang 160 SBT Toán 11 Tập 1: Giá trị đại diện cho nhóm chứa tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên là

A. 625,5.

B. 675,5.

C. 725,5.

D. 775,5.

Lời giải:

Đáp án đúng là: A

Gọi x₁; x₂; x₃;...; x₇₈₇ là mẫu số liệu được xếp theo thứ tự không giảm.

Tứ phân vị thứ nhất của mẫu số liệu x₁; x₂; x₃;...; x₇₈₇ là Q₁ = x₁₉₇. Do x₁₉₇ thuộc nhóm [600,5; 650,5) nên giá trị đại diện cho nhóm chứa tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên là $\frac{1}{2}$(600,5 + 650,5) = 625,5.

Câu 5 trang 160 SBT Toán 11 Tập 1: Giá trị đại diện cho nhóm chứa tứ phân vị thứ ba của mẫu số liệu ghép nhóm trên là

A. 625,5.

B. 675,5.

C. 725,5.

D. 775,5.

Lời giải:

Đáp án đúng là: D

Tứ phân vị thứ ba của mẫu số liệu x₁; x₂; x₃;...; x₇₈₇ là x₅₉₁. Do x₅₉₁ thuộc nhóm [750,5; 800,5) nên giá trị đại diện cho nhóm chứa tứ phân vị thứ ba của mẫu số liệu ghép nhóm trên là $\frac{1}{2}$(750,5 + 800,5) = 775,5.

Trả lời các câu hỏi 6 – 10 dựa trên bảng số liệu về chiều cao của 100 học sinh một trường trung học phổ thông dưới đây.

B. TỰ LUẬN

Bài 1 trang 161 SBT Toán 11 Tập 1: Một công ty bảo hiểm thống kê lại độ tuổi các khách hàng mua bảo hiểm xe ô tô ở bảng sau:

Hãy ước lượng số trung bình, mốt và các tứ phân vị của mẫu số liệu ghép nhóm trên.

Lời giải:

Bảng tần số ghép nhóm bao gồm giá trị đại diện của các nhóm như sau:

Cỡ mẫu n = 233.

• Số trung bình của mẫu số liệu ghép nhóm là:

$\overline{x}=\frac{27,5\cdot 25+32,5\cdot 38+37,5\cdot 62+42,5\cdot 42+47,5\cdot 37+52,5\cdot 29}{233}$ = $\frac{18625}{466}\approx 39,97$.

• Nhóm chứa mốt của mẫu số liệu ghép nhóm là [35; 40)

Do đó, u_m  = 35; n_m‒1 = 38; n_m = 62; n_m+1 = 42; u_{m + 1} ‒ u_m = 40 ‒ 35 = 5.

Mốt của mẫu số liệu ghép nhóm là:

$M_O=35+\frac{62-38}{\left(62-38\right)+\left(62-42\right)}\cdot 5$ = $\frac{415}{11}$.

• Gọi x₁; x₂; x₃;...; x₂₃₃ là mẫu số liệu được xếp theo thứ tự không giảm.

Ta có:

x₁, ..., x₂₅ ∈ [25; 30); x₂₆, ..., x₆₃ ∈ [30; 35); x₆₄, ..., x₁₂₅ ∈ [35; 40);

 x₁₂₆, ..., x₁₆₇ ∈ [40; 45); x₁₆₈, ..., x₂₀₄ ∈ [45; 50); x₂₀₅, ..., x₂₃₃ ∈ [50; 55).

Tứ phân vị thứ hai của mẫu số liệu x₁; x₂; x₃;...; x₂₃₃ là x₁₁₇ ∈ [35; 40). Do đó, tứ phân vị thứ hai của mẫu số liệu ghép nhóm là

$Q_2=35+\frac{\frac{233}{2}-\left(25+38\right)}{62}\cdot \left(40-35\right)$ = $\frac{4875}{124}$.

Tứ phân vị thứ nhất của mẫu số liệu x₁; x₂; x₃;...; x₂₃₃ là $\frac{1}{2}\left(x_{58}+x_{59}\right)$. Do x₅₈ và x₅₉ thuộc nhóm [30; 35) nên tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là

$Q_1=30+\frac{\frac{233}{4}-25}{38}\cdot \left(35-30\right)=\frac{275}{8}$.

Tứ phân vị thứ ba của mẫu số liệu x₁; x₂; x₃;...; x₂₃₃ là $\frac{1}{2}\left(x_{175}+x_{176}\right)$. Do x₁₇₅ và x₁₇₆ thuộc nhóm [45; 50) nên tứ phân vị thứ ba của mẫu số liệu ghép nhóm là

$Q_3=45+\frac{\frac{3\cdot 233}{4}-\left(25+38+62+42\right)}{37}\cdot \left(50-45\right)=\frac{6815}{148}$.

Bài 2 trang 161 SBT Toán 11 Tập 1: Các bạn học sinh một lớp thống kê số túi nhựa mà gia đình bạn đó sử dụng trong một tuần. Kết quả được tổng hợp lại ở bảng sau:

a) Hãy ước lượng số trung bình và mốt của mẫu số liệu trên.

b) Cô giáo dự định trao danh hiệu “Gia đình xanh” cho 25% gia đình các bạn sử dụng ít túi nhựa nhất. Cô giáo nên trao danh hiệu cho các gia đình dùng không quá bao nhiêu túi nhựa?

Lời giải:

a) Do số gia đình là số nguyên nên ta hiệu chỉnh lại bảng số liệu bao gồm giá trị đại diện như sau:

Cỡ mẫu n = 44.

• Số trung bình của mẫu số liệu ghép nhóm là:

$\overline{x}=\frac{7\cdot 8+12\cdot 15+17\cdot 12+22\cdot 7+27\cdot 2}{44}=\frac{162}{11}\approx 14,73$.

• Nhóm chứa mốt của mẫu số liệu ghép nhóm là [9,5; 14,5).

Do đó, u_m  = 9,5; n_m‒1 = 8; n_m = 15; n_m+1 = 12; u_{m + 1} ‒ u_m = 14,5 ‒ 9,5 = 5.

Mốt của mẫu số liệu ghép nhóm là:

$M_0=9,5+\frac{15-8}{\left(15-8\right)+\left(15-12\right)}\cdot 5$ = 13.

b) Gọi x₁; x₂; x₃;...; x₄₄ là mẫu số liệu được xếp theo thứ tự không giảm.

Ta có:

x₁, ..., x₈ ∈ [4,5; 9,5); x₉, ..., x₂₃ ∈ [9,5; 14,5); x₂₄, ..., x₃₅ ∈ [14,5; 19,5);

x₃₆, ..., x₄₂ ∈ [19,5; 24,5); x₄₃, x₄₄ ∈ [24,5; 29,5).

Tứ phân vị thứ nhất của mẫu số liệu x₁; x₂; x₃;...; x₄₄ là $\frac{1}{2}\left(x_{11}+x_{12}\right)$. Do x₁₁ và x₁₂ thuộc nhóm [9,5; 14,5) nên tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là

$Q_1=9,5+\frac{\frac{44}{4}-\left(8+0\right)}{15}\cdot \left(14,5-9,5\right)=\frac{21}{2}$ = 10,5.

Do đó, cô giáo nên trao danh hiệu cho gia đình các bạn dùng không quá 10 túi nhựa.

Bài 3 trang 161 SBT Toán 11 Tập 1: Bảng sau thống kê doanh số bán hàng của các nhân viên một trung tâm thương mại trong một ngày.

a) Hãy ước lượng số trung bình, mốt và trung vị của mẫu số liệu ghép nhóm trên.

b) Trung tâm thương mại dự định sẽ thưởng cho 25% số nhân viên có doanh số bán hàng cao nhất. Theo mẫu số liệu trên, trung tâm thương mại nên khen thưởng các nhân viên có doanh số bán hàng ít nhất là bao nhiêu?

Lời giải:

a) Bảng tần số ghép nhóm bao gồm giá trị đại diện của các nhóm như sau:

Cỡ mẫu n = 36.

• Số trung bình của mẫu số liệu ghép nhóm là:

$\overline{x}=\frac{25\cdot 4+35\cdot 8+45\cdot 12+55\cdot 7+65\cdot 5}{36}=\frac{815}{18}$.

• Nhóm chứa mốt của mẫu số liệu ghép nhóm là [40; 50).

Do đó, u_m  = 40; n_m‒1 = 8; n_m = 12; n_m+1 = 7; u_{m + 1} ‒ u_m = 50 ‒ 40 = 10.

Mốt của mẫu số liệu ghép nhóm là:

$M_O=40+\frac{12-8}{\left(12-8\right)+\left(12-7\right)}\cdot 10=\frac{400}{9}$.

• Gọi x₁; x₂; x₃;...; x₃₆ là mẫu số liệu được xếp theo thứ tự không giảm.

Ta có:

x₁, ..., x₄ ∈ [20; 30); x₅, ..., x₁₂ ∈ [30; 40); x₁₃, ..., x₂₄ ∈ [40; 50); x₂₅, ..., x₃₁ ∈ [50; 60); x₃₂, ..., x₃₆ ∈ [60; 70).

Cỡ mẫu n = 36 là số chẵn nên trung vị $M_e=\frac{1}{2}\left(x_{18}+x_{19}\right)$. Do x₁₈ và x₁₉ thuộc nhóm [40; 50) nên trung vị của mẫu số liệu là

$M_e=40+\frac{\frac{36}{2}-\left(4+8\right)}{12}\cdot \left(50-40\right)$ = 45.

b) Tứ phân vị thứ ba của mẫu số liệu x₁; x₂; x₃; ...; x₃₆ là $\frac{1}{2}\left(x_{27}+x_{28}\right)$. Do x₂₇ và x₂₈ thuộc nhóm [50; 60) nên tứ phân vị thứ ba của mẫu số liệu ghép nhóm là

$Q_3=50+\frac{\frac{3\cdot 36}{4}-\left(4+8+12\right)}{7}\cdot \left(60-50\right)=\frac{380}{7}\approx 54,29$.

Do đó, trung tâm thương mại nên khen thưởng các nhân viên có doanh số bán hàng một ngày ít nhất là 54,29 triệu đồng.

Bài 4 trang 161 SBT Toán 11 Tập 1: Một cửa hàng sách thống kê số truyện thiếu nhi bán được trong hai tháng ở bảng sau:

Hãy ước lượng số trung bình, mốt và các tứ phân vị của mẫu số liệu ghép nhóm trên.

Lời giải:

a) Do số ngày là số nguyên nên ta hiệu chỉnh bảng tần số ghép nhóm bao gồm giá trị đại diện của các nhóm như sau:

Cỡ mẫu n = 61.

• Số trung bình của mẫu số liệu ghép nhóm là:

$\overline{x}=\frac{17\cdot 5+24\cdot 7+31\cdot 25+38\cdot 15+45\cdot 9}{61}=\frac{2003}{61}$.

• Nhóm chứa mốt của mẫu số liệu ghép nhóm là [27,5; 34,5).

Do đó,  u_m  = 27,5; n_m‒1 = 7; n_m = 25; n_m+1 = 15; u_{m + 1} ‒ u_m = 34,5 ‒ 27,5 = 7.

Mốt của mẫu số liệu ghép nhóm là:

$M_o=27,5+\frac{25-7}{\left(25-7\right)+\left(25-15\right)}\cdot 7$ = 32.

• Gọi x₁; x₂; x₃;...; x₆₁ là mẫu số liệu được xếp theo thứ tự không giảm.

Ta có:

x₁, ..., x₅ ∈ [13,5; 20,5); x₆, ..., x₁₂ ∈ [20,5; 27,5); x₁₃, ..., x₃₇ ∈ [27,5; 34,5);

x₃₈, ..., x₅₂ ∈ [34,5; 41,5); x₅₃, ..., x₆₁ ∈ [41,5; 48,5).

Tứ phân vị thứ hai của mẫu số liệu x₁; x₂; x₃;...; x₆₁ là x₃₁. Do x₃₁ ∈ [27,5; 34,5) nên tứ phân vị thứ hai của mẫu số liệu ghép nhóm là

$Q_2=27,5+\frac{\frac{61}{2}-\left(5+7\right)}{25}\cdot \left(34,5-27,5\right)=\frac{817}{25}$ = 32,68.

Tứ phân vị thứ nhất của mẫu số liệu x₁; x₂; x₃;...; x₆₁ là $\frac{1}{2}\left(x_{15}+x_{16}\right)$. Do x₁₅ và x₁₆ thuộc nhóm [27,5; 34,5) nên tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là

$Q_1=27,5+\frac{\frac{61}{4}-\left(5+7\right)}{25}\cdot \left(34,5-27,5\right)=\frac{2841}{100}$ = 28,41.

Tứ phân vị thứ ba của mẫu số liệu x₁; x₂; x₃; ...; x₆₁ là $\frac{1}{2}\left(x_{46}+x_{47}\right)$. Do x₄₆ và x₄₇ thuộc nhóm [34,5; 41,5) nên tứ phân vị thứ ba của mẫu số liệu ghép nhóm là

$Q_3=34,5+\frac{\frac{3\cdot 61}{4}-\left(5+7+25\right)}{15}\cdot \left(41,5-34,5\right)=\frac{463}{12}$.

Bài 5 trang 162 SBT Toán 11 Tập 1: Kết quả điều tra về số giờ làm thêm trong một tuần của 100 sinh viên được cho ở biểu đồ bên.

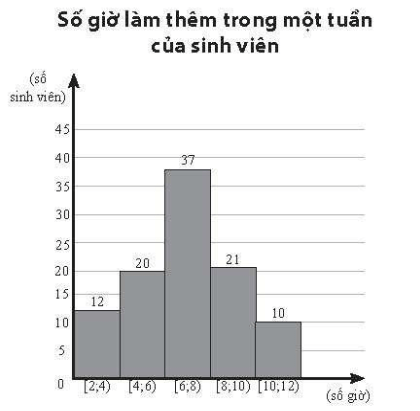
Hãy ước lượng số trung bình, mốt và các tứ phân vị của số liệu đó.

Lời giải:

Từ mẫu số liệu ghép nhóm, ta có bảng thống kê số giờ làm thêm trong một tuần của 100 sinh viên như sau:

Cỡ mẫu n = 100.

Số trung bình của mẫu số liệu ghép nhóm trên là

$\overline{x}=\frac{3\cdot 12+5\cdot 20+7\cdot 37+9\cdot 21+11\cdot 10}{100}$ = 6,94.

Nhóm chứa mốt của mẫu số liệu trên là nhóm [6; 8).

Do đó: u_m = 6; n_m = 37; n_{m ‒ 1} = 20; n_{m + 1} = 21; u_{m + 1} =8.

Vậy mốt của mẫu số liệu ghép nhóm là

$M_O=6+\frac{37-20}{\left(37-20\right)+\left(37-21\right)}\cdot \left(8-6\right)=\frac{232}{33}\approx 7,03$.

Gọi x₁; x₂; ...; x₁₀₀ là mẫu số liệu được xếp theo thứ tự không giảm.

Tứ phân vị thứ hai của mẫu số liệu x₁; x₂; ...; x₁₀₀ là $\frac{1}{2}\left(x_{50}+x_{51}\right)$. Do x₅₀ và x₅₁ thuộc nhóm [6; 8) nên tứ phân vị thứ hai của mẫu số liệu là

$Q_2=6+\frac{\frac{100}{2}-\left(12+20\right)}{37}\cdot \left(8-6\right)=\frac{258}{37}\approx 6,97$.

Tứ phân vị thứ nhất của dãy số liệu x₁; x₂; ...; x₁₀₀ là $\frac{1}{2}\left(x_{25}+x_{26}\right)$. Do x₂₅ và x₂₆ thuộc nhóm [4; 6) nên tứ phân vị thứ nhất của mẫu số liệu là

$Q_1=4+\frac{\frac{100}{4}-\left(12+0\right)}{20}\cdot \left(6-4\right)$ = 5,3.

Tứ phân vị thứ ba của dãy số liệu x₁; x₂; ...; x₁₀₀ là $\frac{1}{2}\left(x_{75}+x_{76}\right)$. Do x₇₅ và x₇₆ thuộc nhóm [8; 10) nên tứ phân vị thứ ba của mẫu số liệu là

$Q_3=8+\frac{\frac{3\cdot 100}{4}-\left(12+20+37\right)}{21}\cdot \left(10-8\right)=\frac{60}{7}\approx 8,57$.

Xem thêm các bài giải SBT Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác: