Cho tam giác MNP có MN = 10, MP = 20 và góc M = 42°. a) Tính diện tích tam giác MNP

Bài 7 trang 75 SBT Toán 10 Tập 1: Cho tam giác MNP có MN = 10, MP = 20 và $\hat{M}$= 42°.

a) Tính diện tích tam giác MNP.

b) Gọi O là tâm đường tròn ngoại tiếp tam giác MNP. Tính diện tích tam giác ONP.

Trả lời

a) Diện tích tam giác MNP là:

S = $\frac{1}{2}$.MN.MP.sin$\hat{M}$= $\frac{1}{2}$.10.20.sin42° ≈ 67 (đvdt).

Vậy diện tích tam giác MNP là 67 đvdt.

b)

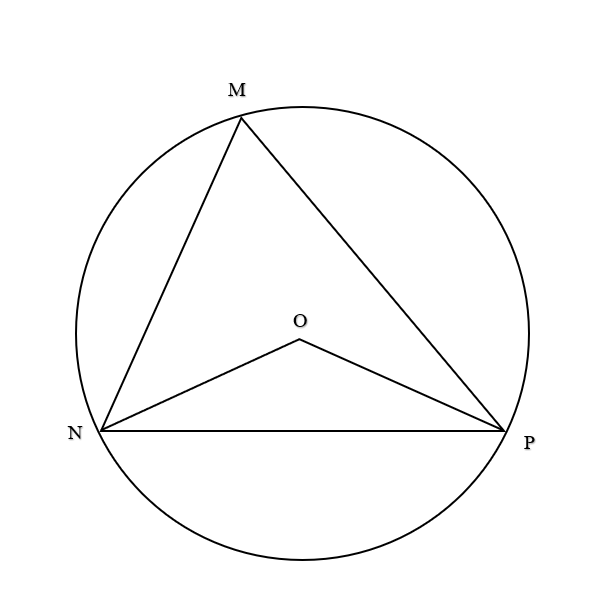
Áp dụng định lí côsin:

NP² = MP² + MN² – 2.MN.MP.cos$\hat{M}$

NP² = 10² + 20² – 2.10.20.cos42°

NP = $\sqrt{{10}^2+{20}^2–\mathrm{2.10.20.}\text{cos}42°}$

NP ≈ 14,24.

Áp dụng định lí sin trong tam giác MNP, ta có: R = ON = OP = $\frac{\text{NP}}{\text{2sin}\widehat{\text{M}}}$ ≈ $\frac{14,24}{2\sin 42°}$ ≈ 10,64

Xét đường tròn tâm O ngoại tiếp tam giác MNP:

$\widehat{\text{NMP}}$ là góc nội tiếp chắn cung NP ⇒ $\widehat{\text{NMP}}$ = $\frac{1}{2}\widehat{\text{NOP}}$ ⇒ $\widehat{\text{NOP}}$ = 42°.2 = 84°.

Suy ra S_ONP = $\frac{1}{2}$.ON.OP.sin$\widehat{\text{NOP}}$ ≈ $\frac{1}{2}$.(10,64)².sin84° ≈ 56,30 (đvdt)

Vậy diện tích tam giác ONP là 56,30 đvdt.

Xem thêm các bài giải SBT Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 3

Bài 1: Giá trị lượng giác của  góc từ 0° đến 180°

Bài 2: Định lí côsin và định lí sin

Bài tập cuối chương 4

Bài 1: Khái niệm vectơ

Bài 2: Tổng và hiệu của hai vectơ