Cho tam giác ABC có trọng tâm G. Chứng minh các tam giác GBC, GAB, GAC có diện tích bằng nhau

Bài 8 trang 75 SBT Toán 10 Tập 1: Cho tam giác ABC có trọng tâm G. Chứng minh các tam giác GBC, GAB, GAC có diện tích bằng nhau.

Trả lời

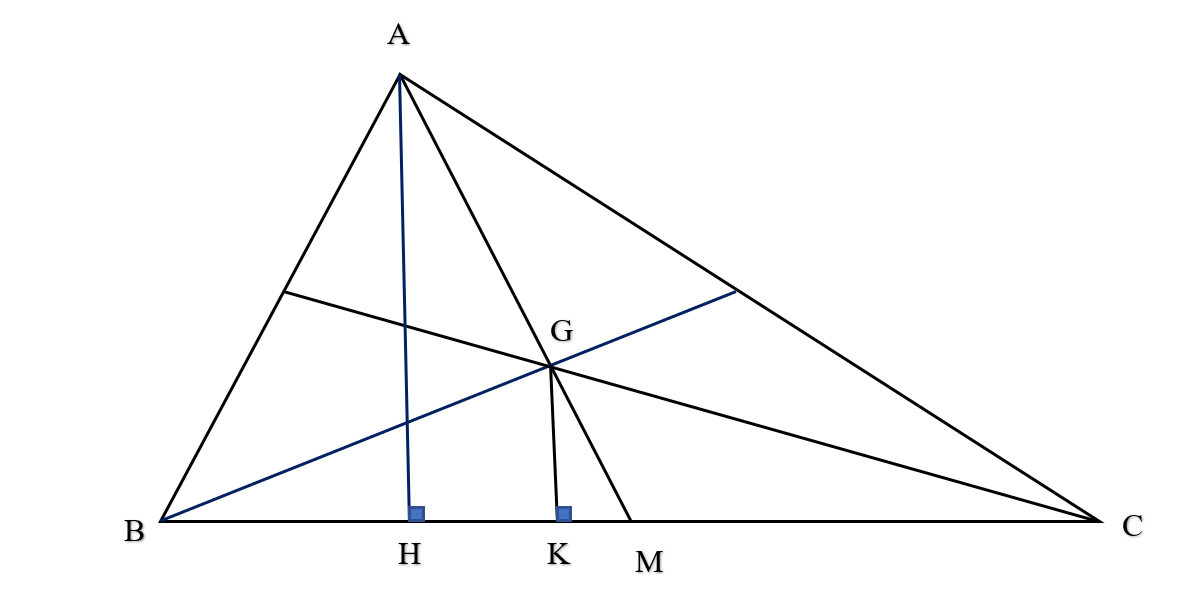
Vẽ AH và GK vuông góc với BC.

Gọi M là chân đường trung tuyến từ A hạ xuống BC. Ta có GM = AM ( tính chất đường trung tuyến của tam giác).

Xét tam giác GKM và tam giác AHM:

$\widehat{\text{AHM}}$ = $\widehat{\text{GKM}}$ = 90°

$\widehat{\text{AMH}}$ = $\widehat{\text{GMK}}$ 

⇒ tam giác GKM và tam giác AHM đồng dạng (g.g).

⇒ $\frac{\text{GM}}{\text{AM}}=\frac{\text{GK}}{\text{AH}}=\frac{1}{3}$

Có $\frac{{\text{S}}_{\text{GBC}}}{{\text{S}}_{\text{ABC}}\text{}}\text{ = }\frac{\frac{\text{1}}{\text{2}}\text{.GK.BC}}{\frac{\text{1}}{\text{2}}\text{.AH.BC}}$ = $\frac{\text{GK}}{\text{AH}}=\frac{1}{3}$.

Chứng minh tương tự ta được:

S_GBC = S_GAB = S_GAC = $\frac{1}{3}$S_ABC. ( ĐPCM).

Xem thêm các bài giải SBT Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 3

Bài 1: Giá trị lượng giác của  góc từ 0° đến 180°

Bài 2: Định lí côsin và định lí sin

Bài tập cuối chương 4

Bài 1: Khái niệm vectơ

Bài 2: Tổng và hiệu của hai vectơ