Giải Sách bài tập Toán 10 Bài 1: Tọa độ của vectơ
Giải SBT Toán 10 trang 61 Tập 2
Bài 1 trang 61 SBT Toán 10 Tập 2: Tọa độ của vectơ →u=−3→i+2→j là:
A. (- 3; 2);
B. (2; - 3);
C. (−3→i;2→j) ;
D. (3; 2).
Lời giải:
Do →u=−3→i+2→j mà →i,→j là các vectơ đơn vị tương ứng với trục Ox và Oy
Nên →u=(−3;2) .
Vậy chọn đáp án A.
Bài 2 trang 61 SBT Toán 10 Tập 2: Tọa độ của vectơ →u=5→j là:
A. (5; 0);
B. (5;→j) ;
C. (0;5→j) ;
D. (0; 5).
Lời giải:
Do →u=5→j mà →i,→j là các vectơ đơn vị tương ứng với trục Ox và Oy
Nên →u=(0;5) .
Vậy chọn đáp án D.
A. (2; 5);
B. (2; - 5);
C. (- 2; - 5);
D. (- 2; 5).
Lời giải:
Tọa độ của vectơ →OA chính là tọa độ điểm A và là: →OA=(2;−5) .
Vậy chọn đáp án B.
A. (1; - 4);
B. (- 3; 4);
C. (3; - 4);
D. (1; - 2).
Lời giải:
Tọa độ của vectơ →AB là hiệu số tọa độ tương ứng của điểm B và điểm A.
Do đó: →AB=(xB−xA;yB−yA)=(2+1;−1−3)=(3;−4) .
Vậy chọn đáp án C.
A. {x=1y=−4 ;
B. {x=−3y=−4 ;
C. {x=1y=4 ;
D. {x=−3y=4 .
Lời giải:
Hai vectơ →u và →v bằng nhau nếu tọa độ tương ứng của chúng bằng nhau
Hay {2x−y=−2y=−4⇔{2x−(−4)=−2y=−4⇔{2x=−6y=−4⇔{x=−3y=−4.
Vậy chọn đáp án B.
A. (8; 3);
B. (3; 8);
C. (- 5; 0);
D. (0; - 5).
Lời giải:
Ta có: →AB=(3+1;2+2)=(4;4)
Gọi D(a; b) thì →DC=(4−a;−1−b)
Do ABCD là hình bình hành nên ta có: →AB=→DC
Hay {4−a=4−1−b=4⇔{a=0b=−5 .
Suy ra D(0; -5).
Vậy chọn đáp án D.
Bài 7 trang 61 SBT Toán 10 Tập 2: Tìm tọa độ của các vectơ trong Hình 4.
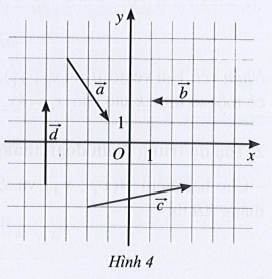
Lời giải:
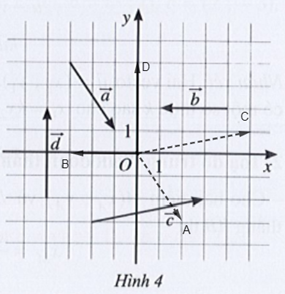
Ta vẽ vectơ →OA=→a, →OB=→b, →OC=→c, →OD=→d .
Quan sát trên hình vẽ, ta có:
A(2; – 3) nên →a=(2;−3) ;
B(– 3; 0) nên →b=(−3;0) ;
C(5; 1) nên →c=(5;1) ;
D(0; 4) nên →d=(0;4) .
Giải SBT Toán 10 trang 62 Tập 2
Bài 8 trang 62 SBT Toán 10 Tập 2: Tìm các số thực a và b sao cho mỗi cặp vectơ sau bằng nhau:
a) →m=(2a+3;b−1) và →n=(1;−2) ;
b) →u=(3a−2;5) và →v=(5;2b+1) ;
c) →x=(2a+b;2b) và →y=(3+2b;b−3a) .
Lời giải:
2 vectơ bằng nhau thì tọa độ tương ứng của chúng phải bằng nhau.
a) Ta có: →m=(2a+3;b−1) và →n=(1;−2) bằng nhau
⇔{2a+3=1b−1=−2⇔{2a=−2b=−1⇔{a=−1b=−1
Vậy a = – 1, b = – 1.
b. Ta có: →u=(3a−2;5) và →v=(5;2b+1) bằng nhau
⇔{3a−2=55=2b+1⇔{3a=72b=4⇔{a=73b=2
Vậy a = 73 , b = 2.
c. Ta có: →x=(2a+b;2b) và →y=(3+2b;b−3a) bằng nhau
⇔{2a+b=3+2b2b=b−3a⇔{2a−b=3b=−3a⇔{2a−(−3a)=3b=−3a⇔{a=35b=−95
Vậy a = 35 và b=−95 .
Lời giải:
Ta có: →AB=(2+4;4−2)=(6;2)
Gọi D(a; b) thì →DC=(8−a;−2−b)
Do ABCD là hình bình hành nên ta có: →AB=→DC
Hay {8−a=6−2−b=2⇔{a=2b=−4 .
Suy ra D(2; -4).
Vậy D(2; -4).
Lời giải:
Ta có: →AB=(xB−xA;yB−yA) ,→DC=(xC−xD;yC−yD)
Do ABCD là hình bình hành nên ta có: →AB=→DC
Hay {xB−xA=xC−xDyB−yA=yC−yD⇔{xB+xD=xC+xAyB+yD=yC+yA
Vậy bài toán được chứng minh.
Lời giải:
Do tứ giác MNPQ là hình thang có MN // PQ
Nên →MN cùng phương với →PQ .
Mà PQ = 2MN, →MN ngược hướng với →PQ
Suy ra →PQ=−2.→MN .
Gọi Q(a; b), ta có: →MN=(3−1;1+2)=(2;3) và →PQ=(a+1;b−2)
→PQ=−2.→MN ⇔{a+1=(−2).2b−2=(−2).3⇔{a=−5b=−4.
Vậy Q(-5; -4).
Xem thêm lời giải sách bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:
Bài 2: Biểu thức tọa độ của các phép toán vectơ
Bài 3: Phương trình đường thẳng
Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng




