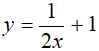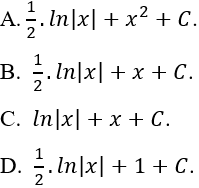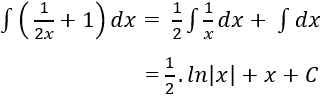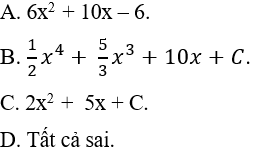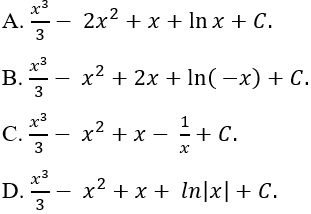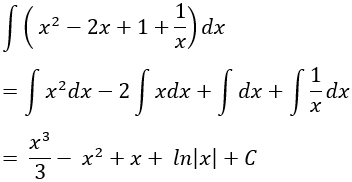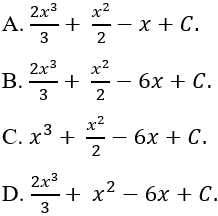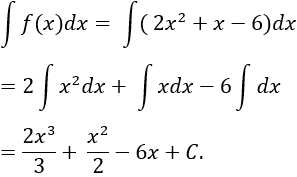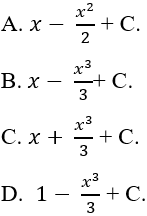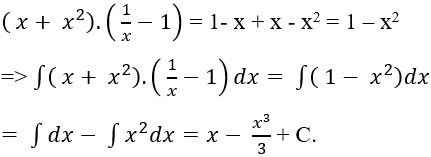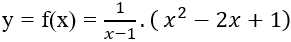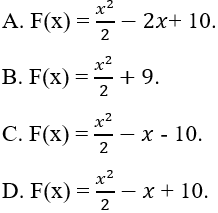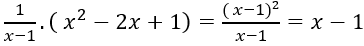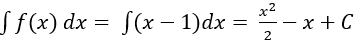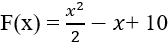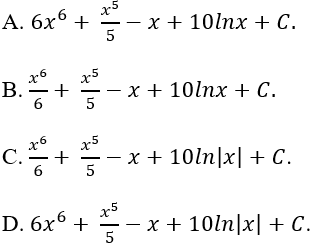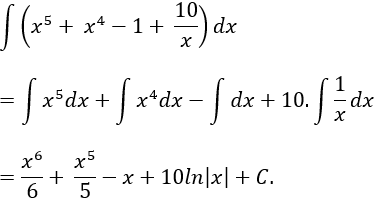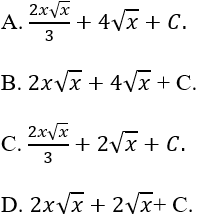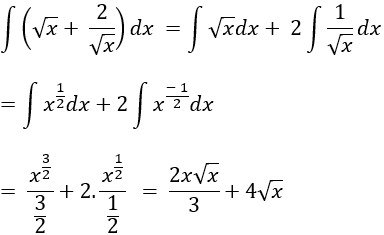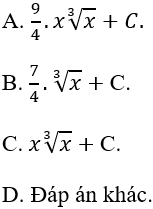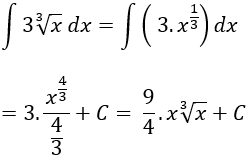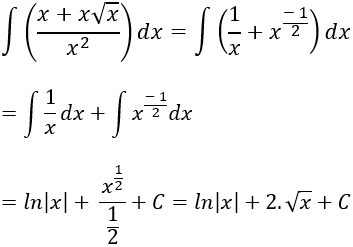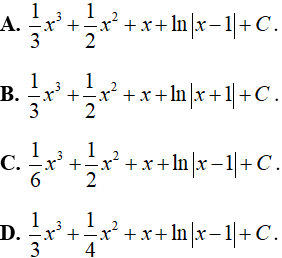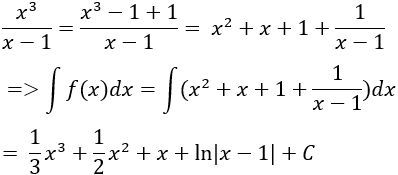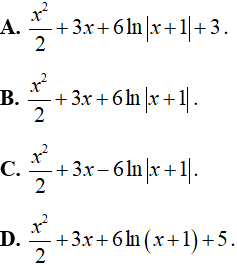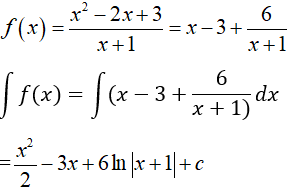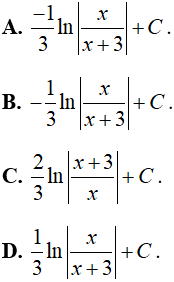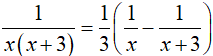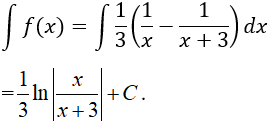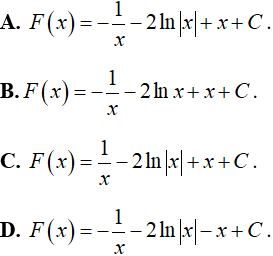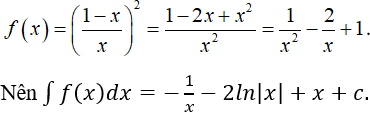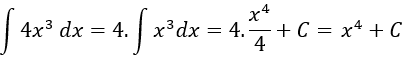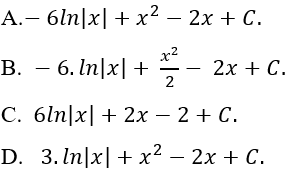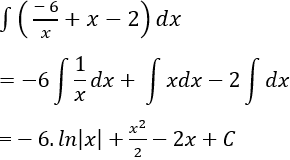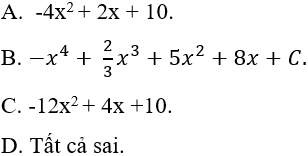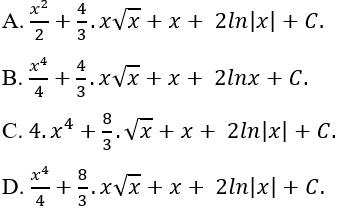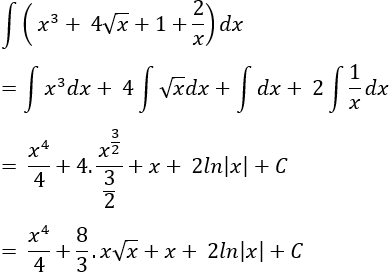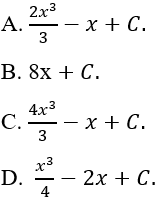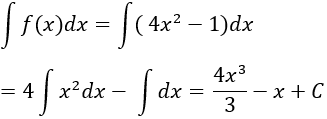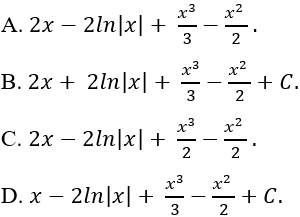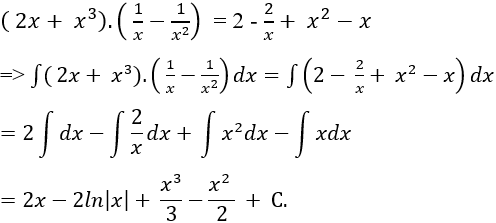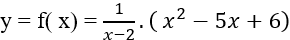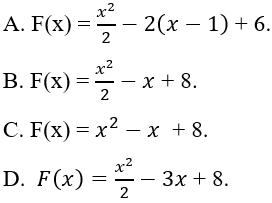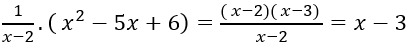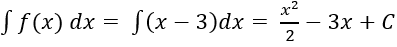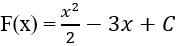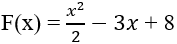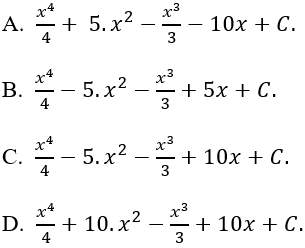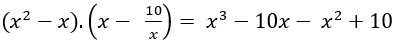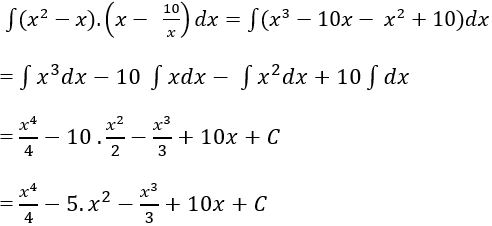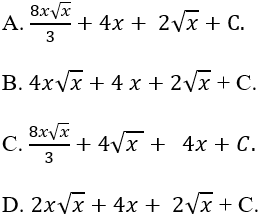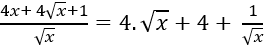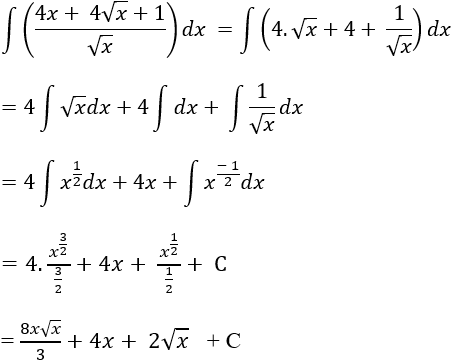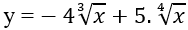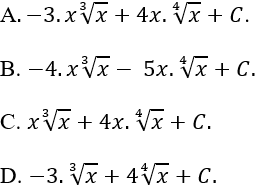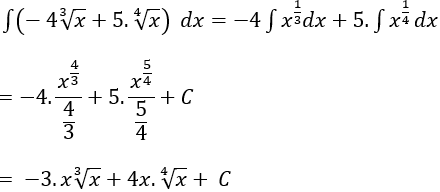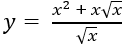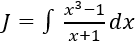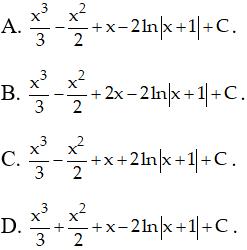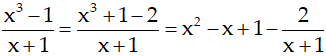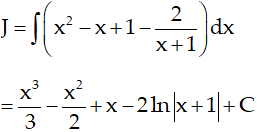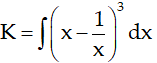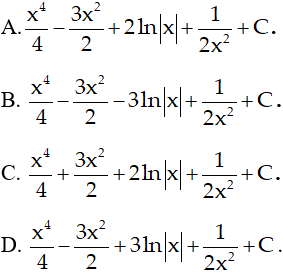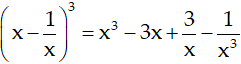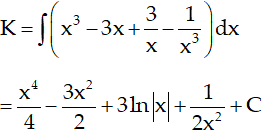Công thức nguyên hàm đa thức (2024) chi tiết nhất

Công thức nguyên hàm đa thức

I. Công thức

Ta có bảng nguyên hàm của các hàm số cơ bản hay gặp

II. Ví dụ minh hoạ

Ví dụ 1. Nguyên hàm của hàm số y = 7x⁶ là:

A. x⁷ + C.

B. x⁶ + C.

C. 42x⁵ + C.

D. 42x⁷ + C.

Hướng dẫn giải:

Nguyên hàm của hàm số đã cho là:

∫7x⁶ dx = x⁷ + C.

Chọn A.

Ví dụ 2. Tính nguyên hàm của hàm số: 

Hướng dẫn giải:

Nguyên hàm của hàm số là:

Chọn B.

Ví dụ 3. Nguyên hàm của hàm số f(x) = 2x + 4 là hàm số nào trong các hàm số sau?

A. x² + 4x + C.

B. 2x² + 4x + C.

C. 2x² + 4 + C.

D. x² + 4 + C.

Hướng dẫn giải:

Ta có: ∫(2x + 4)dx = 2.∫xdx + 4.∫dx = x² + 4x + C.

Chọn A.

Ví dụ 4. Hàm số F(x) = 2x³ + 5x² - 6x + 10 là họ nguyên hàm của hàm số nào sau đây?

Hướng dẫn giải:

Lấy đạo hàm của hàm số F(x) ta được:

F'(x) = 6x² + 10x - 6

⇒ hàm số F(x) là họ nguyên hàm của hàm số: F'(x) = 6x² + 10x - 6

Chọn C.

Ví dụ 5. Họ nguyên hàm của hàm số: 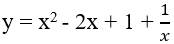 là:

Hướng dẫn giải:

Ta có:

Chọn D.

Ví dụ 6. Tìm nguyên hàm của hàm số f(x) = (x + 2).(2x - 3)

Hướng dẫn giải:

Ta có: (x + 2).(2x - 3) = 2x² - 3x + 4x – 6 = 2x² + x - 6

⇒ Nguyên hàm của hàm số f(x) là:

Chọn B.

Ví dụ 7. Tính ?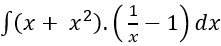

Hướng dẫn giải:

Ta có:

Chọn B.

Ví dụ 8. Cho hàm số:

Gọi F(x) là một nguyên hàm của hàm số f(x) biết F(0) = 10. Tìm hàm F(x).

Hướng dẫn giải:

Điều kiện xác định: x ≠ 1.

Với x ≠ 1 ta có:

Nguyên hàm của hàm số f(x) là:

⇒ Hàm số F(x) cần tìm có dạng 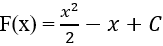 với C là hằng số.

Lại có F(0) = 10 ⇒ C = 10.

Vậy hàm số F(x) cần tìm là:

Chọn D.

Ví dụ 9. Biết một nguyên hàm của hàm số y = f(x) là F(x) = 3x² + 7x - 10. Khi đó, giá trị của hàm số y = f(x) tại x = 1 là:

A. 10.     B. 13.     C. –9.     D. -11.

Hướng dẫn giải:

Do F(x) là một nguyên hàm của hàm số y = f(x) nên ta có:

f(x) = F'(x) = 6x + 7

⇒ f(1) = 13.

Chọn B.

Ví dụ 10. Cho hàm số 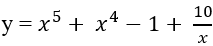. Tìm nguyên hàm của hàm số đã cho.

Hướng dẫn giải:

Nguyên hàm của hàm số đã cho là:

Chọn C.

Ví dụ 11. Tìm nguyên hàm của hàm số: ?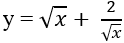

Hướng dẫn giải:

Điều kiện x > 0.

Nguyên hàm của hàm số đã cho là:

Chọn A.

Ví dụ 12. Tìm nguyên hàm của hàm số: 

Hướng dẫn giải:

Ta có:

Chọn A.

Ví dụ 13. Tìm nguyên hàm của hàm số: 

A. ln|x| + 2.√x + C.

B. ln|x| - √x + C.

C. ln|x| + 2.x√x + C.

D. Đáp án khác.

Hướng dẫn giải:

Điều kiện: x > 0.

Ta có: 

⇒ Nguyên hàm của hàm số đã cho là:

Chọn A.

Ví dụ 14. Nguyên hàm của hàm số 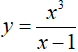 là:

Hướng dẫn giải:

Ta có:

Chọn A.

Ví dụ 15. Một nguyên hàm của hàm số 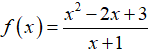 là:

Hướng dẫn giải:

Cho c = 5.

Chọn D.

Ví dụ 16. Kết quả tính 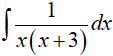 bằng:

Hướng dẫn giải:

Ta có:

Nên:

Chọn D.

Ví dụ 17. Họ nguyên hàm của hàm số 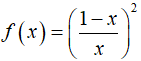 là:

Hướng dẫn giải:

Chọn A.

III. Bài tập vận dụng

Câu 1: Nguyên hàm của hàm số y = 4x³ là:

A. x⁵ + C.

B. x⁴ + C.

C. 12x² + C.

D. 4x² + C.

Lời giải:

Nguyên hàm của hàm số đã cho là:

Chọn B.

Câu 2: Tính nguyên hàm của hàm số: 

Lời giải:

Nguyên hàm của hàm số là:

Chọn B.

Câu 3: Nguyên hàm của hàm số f(x) = -4x + 4 là hàm số nào trong các hàm số sau?

A. -4x² + 4x + C.

B. 2x² + 4x + C.

C. -2x² + 4x + C.

D. x² + 4 + C.

Lời giải:

Ta có: ∫(-4x + 4)dx = -4.∫xdx + 4.∫dx = -2x² + 4x + C.

Chọn C.

Câu 4: Hàm số F(x) = -4x³ + 2x² + 10x + 8 là họ nguyên hàm của hàm số nào sau đây?

Lời giải:

Lấy đạo hàm của hàm số F(x) ta được:

 

F'(x) = -12x² + 4x + 10

⇒ Hàm số F(x) là họ nguyên hàm của hàm số: F'(x) = -12x² + 4x + 10

Chọn C.

Câu 5: Họ nguyên hàm của hàm số 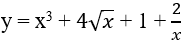 là:

Lời giải:

Ta có:

Chọn D.

Câu 6: Tìm nguyên hàm của hàm số f(x) = (2x - 1)(2x + 1)

Lời giải:

Ta có: (2x - 1).(2x + 1) = 4x² - 1

⇒ Nguyên hàm của hàm số f(x) là:

Chọn C.

Câu 7: Tính  ?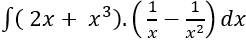

Lời giải:

Ta có:

Chọn A.

Câu 8: Cho hàm số:

Gọi F(x) là một nguyên hàm của hàm số f(x) biết F(0) = 8. Tìm hàm F(x).

Lời giải:

Điều kiện xác định: x ≠ 2 và x ≠ 3.

Với x ≠ 2; 3 ta có:

Nguyên hàm của hàm số f(x) là:

⇒ Hàm số F(x) cần tìm có dạng:

với C là hằng số.

Lại có F(0) = 8 ⇒ C = 8.

Vậy hàm số F(x) cần tìm là:

Chọn D.

Câu 9: Biết một nguyên hàm của hàm số y = f(x) là F(x) = 4x⁶ + 7x² - 10x. Khi đó, giá trị của hàm số y = f(x) tại x = -1 là:

A. 36.

B. 48.

C. –48.

D. -36.

Lời giải:

Do F(x) là một nguyên hàm của hàm số y = f(x) nên ta có:

f(x) = F'(x) = 24x⁵ + 14x - 10

⇒ f(-1) = -48.

Chọn C.

Câu 10: Cho hàm số 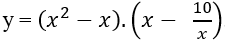. Tìm nguyên hàm của hàm số đã cho.

Lời giải:

Điều kiện: x ≠ 0.

Ta có:

Nguyên hàm của hàm số đã cho là:

Chọn C.

Câu 11: Tìm nguyên hàm của hàm số  ?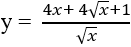

Lời giải:

Điều kiện: x > 0.

Ta có:

Nguyên hàm của hàm số đã cho là:

Chọn A.

Câu 12: Tìm nguyên hàm của hàm số:

Lời giải:

Ta có:

Chọn A.

Câu 13: Tìm nguyên hàm của hàm số: 

Lời giải:

Điều kiện: x > 0.

Ta có:

⇒ Nguyên hàm của hàm số đã cho là:

Chọn A.

Câu 14: Tìm nguyên hàm của hàm số: 

Lời giải:

Ta có:

Suy ra:

Chọn A.

Câu 15: Tìm nguyên hàm của hàm số 

Lời giải:

Ta có:

Suy ra:

Chọn D.

Xem thêm các dạng bài tập hay, có đáp án:

30 Bài tập Tìm nguyên hàm của hàm đa thức bằng phương pháp đổi biến số (2024) cực hay, có đáp án

30 Bài tập Tìm nguyên hàm của hàm chứa căn thức bằng phương pháp đổi biến số (2024) cực hay, có đáp án

30 Bài tập tìm nguyên hàm của hàm số lượng giác (2024) có đáp án chi tiết

30 Bài tập Tìm nguyên hàm của hàm số lượng giác bằng phương pháp đổi biến số (2024) cực hay, có đáp án

30 Bài tập Tìm nguyên hàm của hàm số mũ, logarit bằng phương pháp đổi biến số (2024) cực hay, có đáp án