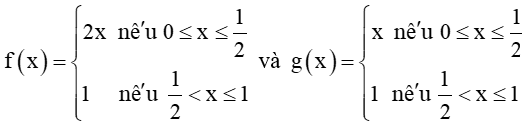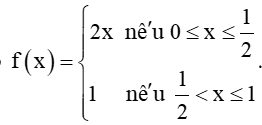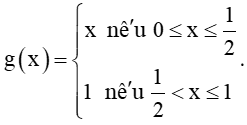Xét tính liên tục của các hàm số f(x) và g(x) tại điểm x=1/2 và nhận xét về sự khác nhau giữa hai đồ thị

HĐ2 trang 120 Toán 11 Tập 1: Cho hai hàm số 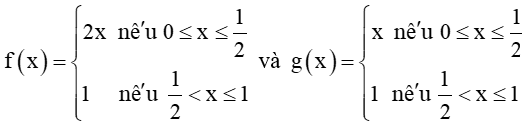 với đồ thị tương ứng như Hình 5.7.

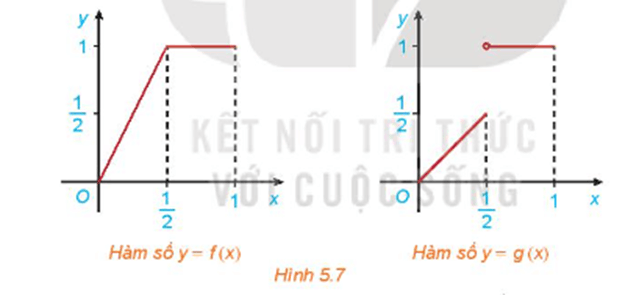
Xét tính liên tục của các hàm số f(x) và g(x) tại điểm $x=\frac{1}{2}$ và nhận xét về sự khác nhau giữa hai đồ thị.

Trả lời

+) Hàm số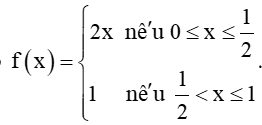

Hàm số f(x) xác định trên [0; 1], do đó $x=\frac{1}{2}$ thuộc tập xác định của hàm số.

Ta có: $\underset{x\to {\frac{1}{2}}^{+}}{\lim }f\left(x\right)=\underset{x\to {\frac{1}{2}}^{+}}{\lim }1=1$; $\underset{x\to {\frac{1}{2}}^{-}}{\lim }f\left(x\right)=\underset{x\to {\frac{1}{2}}^{-}}{\lim }\left(2x\right)=2\cdot \frac{1}{2}=1$.

Suy ra $\underset{x\to {\frac{1}{2}}^{+}}{\lim }f\left(x\right)=\underset{x\to {\frac{1}{2}}^{-}}{\lim }f\left(x\right)=1$, do đó $\underset{x\to \frac{1}{2}}{\lim }f\left(x\right)=1$

Mà $f\left(\frac{1}{2}\right)=2\cdot \frac{1}{2}=1$ nên $\underset{x\to \frac{1}{2}}{\lim }f\left(x\right)=f\left(\frac{1}{2}\right)$.

Vậy hàm số f(x) liên tục tại $x=\frac{1}{2}$.

+) Hàm số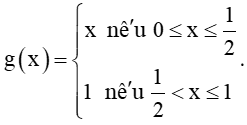 

Hàm số g(x) liên tục trên [0; 1], do đó $x=\frac{1}{2}$ thuộc tập xác định của hàm số.

Ta có: $\underset{x\to {\frac{1}{2}}^{-}}{\lim }g\left(x\right)=\underset{x\to {\frac{1}{2}}^{-}}{\lim }x=\frac{1}{2}$; $\underset{x\to {\frac{1}{2}}^{+}}{\lim }g\left(x\right)=\underset{x\to {\frac{1}{2}}^{+}}{\lim }1=1$

Suy ra $\underset{x\to {\frac{1}{2}}^{+}}{\lim }g\left(x\right)\ne \underset{x\to {\frac{1}{2}}^{-}}{\lim }g\left(x\right)$.

Vậy không tồn tại giới hạn của hàm số g(x) tại $x=\frac{1}{2}$, do đó hàm số g(x) gián đoạn tại $x=\frac{1}{2}$.

+) Quan sát Hình 5.7 ta thấy, đồ thị của hàm số y = f(x) là đường liền trên (0; 1), còn đồ thị của hàm số y = g(x) trên (0; 1) là các đoạn rời nhau.

Xem thêm các bài giải SGK Toán 11 Kết nối tri thức hay, chi tiết khác:

Bài 15: Giới hạn của dãy số

Bài 16: Giới hạn của hàm số

Bài 17: Hàm số liên tục

Bài tập cuối Chương 5

Một vài áp dụng của toán học trong tài chính

Lực căng mặt ngoài của nước