Xét số phức z thỏa mãn $\left|z-1-i\right|=5$ . Khi $\left|z-7-9i\right|+2\left|z-8i\right|$  đạt giá trị nhỏ nhất, $\left|z-1\right|$  bằng

Đáp án đúng là: C

Đặt z = x + yi và gọi M là điểm biểu diễn số phức z trên mặt phẳng phức.

Khi đó bài toán trở thành tìm M thuộc đường tròn $\left(C\right):\left\{\begin{array}{c}I\left(1;1\right)\\ R=5\end{array}\right.$  sao cho MA + 2MB đạt giá trị nhỏ nhất với A(7;9), (B(0;8).

Ta có $\overrightarrow{IA}=\left(6;8\right)\Rightarrow IA=10=2R$ . Ta cần tìm điểm K sao cho MA = 2MK.

Ta có IA = 2R

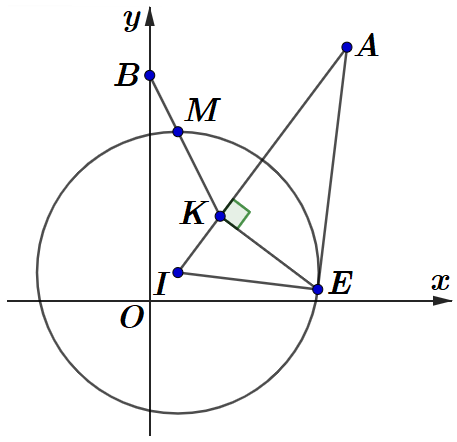
Kẻ tiếp tuyến EA của (C), khi đó tam giác AEI vuông tại E, kẻ đường cao EK của tam giác AEI. Khi đó tam giác AEI đồng dạng với tam giác EKI.

$\Rightarrow \frac{EI}{KI}=\frac{AI}{EI}=2\iff KI=\frac{EI}{2}$$\Rightarrow KI=\frac{1}{4}AI\Rightarrow K\left(\frac{5}{2};3\right)$

Khi đó $MA+2MB=2MK+2MB\ge 2KB$ .

Đẳng thức xảy ra khi M là giao điểm của BK với (C).

Ta có $BK:\left\{\begin{array}{c}x=t\\ y=8-2t\end{array}\right.\Rightarrow M\left(t;8-2t\right)$ .

Ta có $M\in \left(C\right)\Rightarrow {\left(t-1\right)}^2+{\left(7-2t\right)}^2=5\iff \left[\begin{array}{c}t=1\Rightarrow x=1\left(n\right)\\ t=5\Rightarrow x=5\left(l\right)\end{array}\right.$

$\Rightarrow M\left(1;6\right)\Rightarrow z=1+6i\Rightarrow \left|z-1\right|=6$.