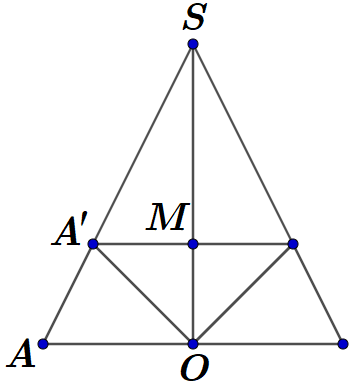
Cho hình nón (N) có đường cao SO = h và bán kính đáy bằng R, gọi M là điểm trên đoạn SO, đặt OM = x (0 < x < h).
Cho hình nón (N) có đường cao SO = h và bán kính đáy bằng R, gọi M là điểm trên đoạn SO, đặt OM = x (0 < x < h). Gọi (C) là thiết diện của hình nón (N) cắt bởi mặt phẳng (P) vuông góc với trục SO tại M. Tìm x để thể tích khối nón đỉnh O đáy là (C) lớn nhất.
A. h√32
B. h2
C. h3
D. h√22