Xét các số phức z, w thỏa mãn |z| = 3, |iw + 1 – 5i| = 4. Giá trị nhỏ nhất của $\left|z^2+wz-9\right|$  bằng

Đáp án đúng là: C

Ta có $\left|iw+1-5i\right|=4\iff \left|-w+5+i\right|=4$ .

Đặt u = -w suy ra |u + 5 +i| = 4. Do đó u thuộc đường tròn tâm I(-5;-1) bán kính bằng R = 4.

Giả sử z = a + bi với $a,b\in ℝ$ .

Vì |z| = 3 nên $a^2+b^2=9\Rightarrow b^2\le 9\Rightarrow -3\le b\le 3$ .

Khi đó $T=\left|z^2+wz-9\right|=\left|z^2+wz-z\overline{z}\right|=\left|z\right|\left|z-\overline{z}+w\right|=3\left|u-2bi\right|$ .

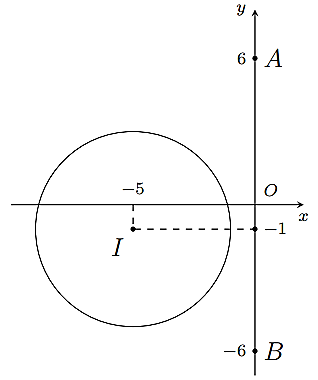
Tập hợp các điểm biểu diễn số phức 2bi là đoạn AB.

Do đó $T_{\min }=3\left(\text{d}\left(I,AB\right)-R\right)=3$ .