Lời giải
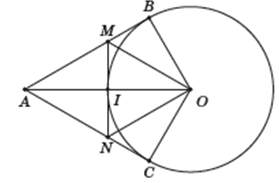
1) Tứ giác AMON có: AM // ON (cùng vuông góc với OB) và AC // OM (cùng vuông góc với OC).
Suy ra tứ giác AMON là hình bình hành (1)
Xét ∆OBM và ∆OCN, có:
\[\widehat {MBO} = \widehat {NCO} = 90^\circ \];
OB = OC (= R);
\(\widehat {MOB} = \widehat {NOC}\) (cùng phụ với \(\widehat {MON}\)).
Do đó ∆OBM = ∆OCN (g.c.g).
Suy ra OM = ON (cặp cạnh tương ứng) (2)
Từ (1), (2), suy ra tứ giác AMON là hình thoi.
2) Gọi I là giao điểm của AO và MN.
Suy ra AO ⊥ MN tại I và I là trung điểm AO và MN (do tứ giác AMON là hình thoi).
MN tiếp xúc với (O; R) khi và chỉ khi d(O, MN) = R.
⇔ OI = R.
⇔ OA = 2R (do I là trung điểm AO).
Vậy OA = 2R thỏa mãn yêu cầu bài toán.
3) Tam giác ABO vuông tại B: \(\sin \widehat {OAB} = \frac{{OB}}{{OA}} = \frac{R}{{2R}} = \frac{1}{2}\).
\( \Rightarrow \widehat {OAB} = 30^\circ \).
Ta có \(\widehat {AON} = \widehat {OAB} = 30^\circ \) (AM // ON và cặp góc này là cặp góc so le trong).
Tam giác OIN vuông tại I: \(\tan \widehat {AON} = \frac{{IN}}{{OI}}\).
Suy ra \(IN = R.\tan 30^\circ = \frac{{R\sqrt 3 }}{3}\).
Do đó \(MN = \frac{{2R\sqrt 3 }}{3}\).
Vậy diện tích hình thoi AMON là: \({S_{AMON}} = \frac{1}{2}OA.MN = \frac{1}{2}.2R.\frac{{2R\sqrt 3 }}{3} = \frac{{2{R^2}\sqrt 3 }}{3}\).

