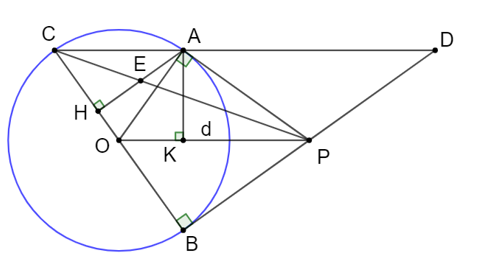
Từ điểm P nằm ngoài đường tròn tâm O bán kính R, kẻ hai tiếp tuyến PA, PB tới đường tròn (A, B là các tiếp điểm). Gọi H là chân đường vuông góc
Từ điểm P nằm ngoài đường tròn tâm O bán kính R, kẻ hai tiếp tuyến PA, PB tới đường tròn (A, B là các tiếp điểm). Gọi H là chân đường vuông góc kẻ từ A tới đường kính BC, đoạn thẳng PC cắt AH tại E.
a) Chứng minh bốn điểm P, A, O, B cùng nằm trên một đường tròn.