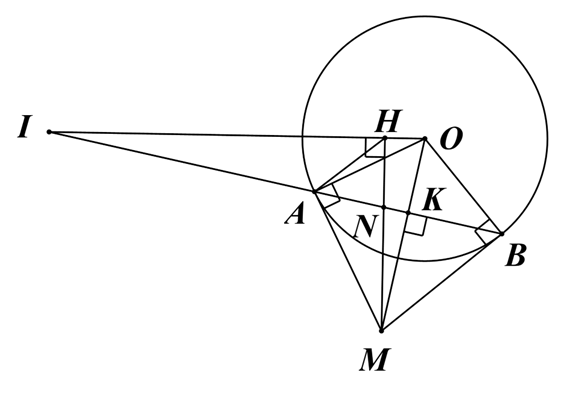
a) Ta có MA, MB là hai tiếp tuyến của (O) cắt nhau tại M.

Suy ra MA = MB.

Khi đó M nằm trên đường trung trực của đoạn thẳng AB (1)

Lại có OA = OB =R.

Suy ra O nằm trên đường trung trực của đoạn thẳng AB (2)

Từ (1), (2), suy ra MO là đường trung trực của đoạn thẳng AB.

Do đó MO ^ AB tại K và K là trung điểm AB.

b) Xét ∆OHM và ∆OKI, có:

\(\widehat O\) chung.

\[\widehat {OHM} = \widehat {OKI} = 90^\circ \]

Do đó ∆OHM ᔕ ∆OKI (g.g).

Suy ra \(\frac{{OH}}{{OK}} = \frac{{OM}}{{OI}}\).

Do đó OH.OI = OM.OK.

Xét ∆AOM vuông tại A có AK là đường cao:

OA² = OK.OM (hệ thức lượng trong tam giác vuông).

Vậy OH.OI = OA² = OB² (điều phải chứng minh).

c) Ta có \[\widehat {OAM} = 90^\circ \;\left( {gt} \right)\]

Suy ra O, A, M nội tiếp đường tròn đường kính OM.

Tương tự, ta có O, H, M nội tiếp đường tròn đường kính OM.

Khi đó tứ giác AHOM nội tiếp đường tròn đường kính OM.

Suy ra \(\widehat {AMO} = \widehat {AHI}\)(1)

Ta có \[\widehat {OAM} = \widehat {OBM} = 90^\circ \](MA, MB là các tiếp tuyến của đường tròn (O)).

Suy ra \[\widehat {OAM} + \widehat {OBM} = 180^\circ \]

Do đó tứ giác OAMB nội tiếp đường tròn đường kính OM.

Vì \[\widehat {AMO} = \widehat {ABO}\](cùng chắn cung ) (2)

Từ (1), (2), suy ra \[\widehat {ABO} = \widehat {AHI}\]

Xét ∆IHN và ∆IKO, có:

\[\widehat I\] chung.

\[\widehat {IHN} = \widehat {IKO} = 90^\circ \]

Do đó ∆IHN ᔕ ∆IKO (g.g).

Suy ra \(\frac{{IH}}{{IK}} = \frac{{IN}}{{IO}}\)

Do đó IH.IO = IN.IK   (3)

Xét ∆AHI và ∆OBI, có:

\[\widehat I\]chung.

\[\widehat {ABO} = \widehat {AHI}\](chứng minh trên).

Do đó ∆AHI ᔕ ∆OBI (g.g).

Suy ra \[\frac{{IA}}{{IO}} = \frac{{IH}}{{IB}}\].

Do đó IA.IB = IH.IO (4)

Từ (3), (4), suy ra IA.IB = IN.IK (điều phải chứng minh).