Từ điểm A nằm ngoài đường tròn (O). Vẽ hai tiếp tuyến AB, AC (B, C là hai tiếp điểm). Từ điểm K nằm trên cung BC (K, A nằm cùng phía BC) dựng tiếp tuyến cắt AB, AC tại M, N. BC cắt OM, ON tại

Trả lời

Lời giải

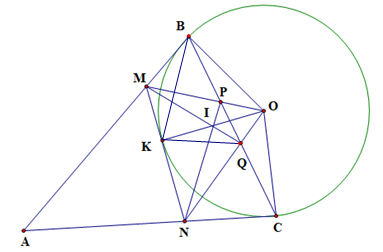
Vì AB, AC là tiếp tuyến của (O) nên \(\widehat {ABO} = \widehat {AC{\rm{O}}} = 90^\circ \).

Vì MN là tiếp tuyến của (O) tại tiếp điểm K nên \(\widehat {OKM} = 90^\circ \).

Xét tứ giác MBOK có: \(\widehat {OBM} = \widehat {OKM} = 90^\circ \), mà hai góc này ở vị trí đối nhau trong tứ giác

Þ tứ giác MBOK nội tiếp.

\( \Rightarrow \widehat {MKB} = \widehat {MOB}\) (hai góc nội tiếp cùng chắn cung MB). (1)

Ta có: NK, NC là hai tiếp tuyến của (O) cắt nhau tại N

Þ NK = NC và NQ là tia phân giác của \(\widehat {KNC}\)

Từ đó DNKQ = DNCQ (c.g.c)

\( \Rightarrow \widehat {NKQ} = \widehat {NCQ}\) (hai góc tương ứng)

Lại có \(\widehat {NCQ} = \widehat {ACB} = \widehat {ABC}\) (do DABC cân tại A vì AB = AC)

\( \Rightarrow \widehat {NKQ} = \widehat {ABC}\) hay \(\widehat {NKQ} = \widehat {MBQ}\).

Mà \(\widehat {NKQ} + \widehat {MKQ} = 180^\circ \Rightarrow \widehat {MBQ} + \widehat {MKQ} = 180^\circ \)

Xét tứ giác MBQK có: \(\widehat {MBQ} + \widehat {MKQ} = 180^\circ \) và hai góc này ở vị trí đối nhau trong tứ giác

Þ tứ giác MBQK nội tiếp

\( \Rightarrow \widehat {MKB} = \widehat {MQB}\) (hai góc nội tiếp cùng chắn cung MB). (2)

Từ (1) và (2) suy ra \(\widehat {MQB} = \widehat {MOB}\).

Þ tứ giác MBOQ nội tiếp.

Chứng minh tương tự ta cũng có: tứ giác NCOP là tứ giác nội tiếp.