Trong tam giác ABC lấy điểm O sao cho góc ABO= góc ACO. Gọi H, K lần lượt là hình chiếu của O lên AB, AC

Đề bài. Trong tam giác ABC lấy điểm O sao cho $\widehat{ABO}=\widehat{ACO}$. Gọi H, K lần lượt là hình chiếu của O lên AB, AC. Gọi M là trung điểm của BC. Chứng minh tam giác MHK là tam giác cân.

Trả lời

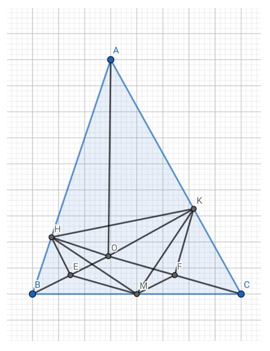ΔHOB vuông tại H và ΔKOC vuông tại K có:

$\widehat{HBO}=\widehat{KCO} (\widehat{ABO}=\widehat{ACO}):gt)$

⇒ $\widehat{HOB}=\widehat{KOC}$ (1)

Gọi E, F lần lượt là trung điểm OB, OC

Xét ΔHOB vuông tại H có:

E là trung điểm cạnh huyền OB

⇒ EO = EH = EB

⇒ΔEOH cân tại E

⇒ $\widehat{HEO}={180}^{\circ }-2\widehat{EOH}$(2)

Xét ΔKOC vuông tại K có:

F là trung điểm cạnh huyền OC

⇒ FO = FK = FC

⇒ΔFOK cân tại F

⇒ $\widehat{KFO}={180}^{\circ }-2\widehat{FOK}$(3)

(1), (2), (3) ⇒ $\widehat{KFO}=\widehat{HEO}$

Mặt khác:

ΔOBC có: M,E,F lần lượt là trung điểm BC,OB,OC

⇒ OEMF là hình bình hành

⇒ OE = MF; OF = ME; $\widehat{OEM}=\widehat{OFM}$

⇒ HE = MF, KF = ME; $\widehat{HEO}+\widehat{OEM}=\widehat{KFO}+\widehat{OFM}$

⇒ $\widehat{HEM}=\widehat{KFM}$

Xét ΔHEM và ΔMFK có:

HE = MF(cmt)

$\widehat{HEM}=\widehat{KFM}$

ME = KF(cmt)

Do đó ΔHEM = ΔMFK (c.g.c)

⇒ MH = MK

⇒ ΔMHK cân tại M