Câu 19: Trong lớp 10C có 16 học sinh giỏi Toán, 15 học sinh giỏi Lí, 11 học sinh giỏi Hóa. Biết rằng có 9 học sinh vừa giỏi Toán và Lí, 6 học sinh vừa giỏi Lí và Hóa, 8 học sinh vừa giỏi Hóa và Toán, trong đó có 11 học sinh giỏi đúng 2 môn. Hỏi có bao nhiêu học sinh trong lớp:
a) Giỏi cả ba môn.
b) Giỏi đúng 1 môn.
a) Gọi A là tập hợp số học sinh giỏi Toán. Tức là, n(A) = 16.
B là tập hợp số học sinh giỏi Lí. Tức là, n(B) = 15.
C là tập hợp số học sinh giỏi Hóa. Tức là, n(C) = 11.
Có 9 học sinh vừa giỏi Toán và Lí. Suy ra n(A ∩ B) = 9.
Có 6 học sinh vừa giỏi Lí và Hóa. Suy ra n(B ∩ C) = 6.
Có 8 học sinh vừa giỏi Hóa và Toán. Suy ra n(A ∩ C) = 8.
Ta có sơ đồ Ven:
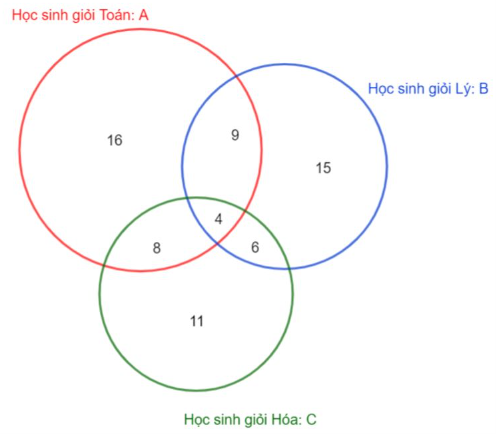
Vì có 11 học sinh chỉ giỏi đúng 2 môn nên ta có:
n(A ∩ B) + n(B ∩ C) + n(C ∩ A) – 3.n(A ∩ B ∩ C) = 11.
⇒ 9 + 6 + 8 – 3.n(A ∩ B ∩ C) = 11.
⇔ n(A ∩ B ∩ C) = 4.
Vậy có 4 học sinh trong lớp 10C giỏi cả ba môn.
b) Xét tổng n(A) + n(B) + n(C), có:
⦁ n(A ∩ B) + n(B ∩ C) + n(A ∩ C) được tính 2 lần nên ta phải trừ đi 1 lần;
⦁ n(A ∩ B ∩ C) được tính 3 lần nên ta phải trừ đi 2 lần.
Trong n(A ∩ B) + n(B ∩ C) + n(A ∩ C), có n(A ∩ B ∩ C) được tính 3 lần, trừ đi 1 lần n(A ∩ B) + n(B ∩ C) + n(A ∩ C) là trừ đi 3 lần n(A ∩ B ∩ C).
Như vậy, số học sinh chỉ giỏi một môn là:
n(A ∪ B ∪ C)
= n(A) + n(B) + n(C) – [n(A ∩ B) + n(A ∩ C) + n(B ∩ C)] + n(A ∩ B ∩ C).
= 16 + 15 + 11 – (9 + 8 + 6) + 4 = 23.