Trong Hình 94, đường thẳng CD là đường trung trực của đoạn thẳng AB. Chứng minh góc CAD = góc CBD
Bài 1 trang 103 Toán 7 Tập 2: Trong Hình 94, đường thẳng CD là đường trung trực của đoạn thẳng AB. Chứng minh ^CAD=^CBD.
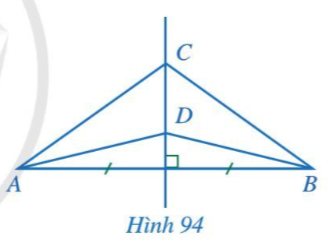
Bài 1 trang 103 Toán 7 Tập 2: Trong Hình 94, đường thẳng CD là đường trung trực của đoạn thẳng AB. Chứng minh ^CAD=^CBD.

|
GT |
CD là đường trung trực của đoạn thẳng AB |
|
KL |
^CAD=^CBD |
Chứng minh (Hình vẽ dưới đây):
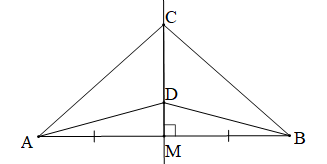
Gọi M là giao điểm của CD và AB. Khi đó M là trung điểm của AB.
CD là đường trung trực của đoạn thẳng AB nên:
+) C thuộc đường trung trực của đoạn thẳng AB do đó CA = CB.
+) D thuộc đường trung trực của đoạn thẳng AB do đó DA = DB.
Xét ∆CAD và CBD có:
CD là cạnh chung,
CA = AB (chứng minh trên),
DA = DB (chứng minh trên)
Do đó CAD = CBD (c.c.c)
Do đó (hai góc tương ứng)
Vậy .
Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:
Bài 8: Đường vuông góc và đường xiên
Bài 9: Đường trung trực của một đoạn thẳng
Bài 10: Tính chất ba đường trung tuyến của tam giác