Trên đường tròn (O; R) vẽ dây cung BC cố định. Một điểm A di chuyển trên cung lớn BC. Hai đường cao AE và BF của tam giác ABC cắt nhau tại H. a) Chứng minh tứ giác ABEF nội tiếp. b) Chứng min
25
19/05/2024
Trên đường tròn (O; R) vẽ dây cung BC cố định. Một điểm A di chuyển trên cung lớn BC. Hai đường cao AE và BF của tam giác ABC cắt nhau tại H.
a) Chứng minh tứ giác ABEF nội tiếp.
b) Chứng minh tam giác ABC đồng dạng tam giác EFC.
c) Đường thẳng AE cắt đường tròn (O) tại I. Chứng minh H và I đối xứng nhau qua BC.
d) Gọi K là hình chiếu của O trên BC. Chứng minh tỉ số \[\frac{{AH}}{{OK}}\] không đổi và H chạy trên một cung tròn cố định khi A chuyển động trên cung lớn BC.
Trả lời
Lời giải
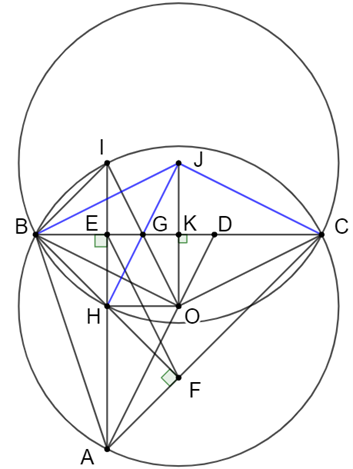
a) Tứ giác ABEF có 2 đỉnh kề nhau cùng nhìn cung BA với hai góc bằng nhau:
\(\widehat {BEA} = \widehat {AFB} = 90^\circ \).
Do đó tứ giác ABEF nội tiếp đường tròn.
b) Tứ giác EBAF nội tiếp đường tròn.
\( \Rightarrow \widehat {BAE} = \widehat {BFE}\) (Hai góc nội tiếp cùng chắn cung BE).
Lại có: \(\widehat {BAE} = 90^\circ - \widehat {EBA}\)
Và \(\widehat {BFE} = 90^\circ - \widehat {EFC}\)
\( \Rightarrow \widehat {EFC} = \widehat {EBA} \Rightarrow \widehat {CBA} = \widehat {CFE}\)
Xét ∆ABC và ∆EFC có:
\(\widehat {CBA} = \widehat {CFE}\) (cmt)
\(\widehat C\): góc chung
Þ ∆ABC ᔕ ∆EFC (g.g)
c) Ta có: \(\widehat {IBC} = \widehat {IAC}\) (Hai góc nội tiếp cùng chắn cung IC)
Lại có: \(\widehat {EBF} = \widehat {EAF}\) (Hai góc nội tiếp cùng chắn cung EF)
Þ \(\widehat {IBE} = \widehat {HBE}\)
Þ BE là đường phân giác của góc \(\widehat {IBH}\).
Mà BE cũng là đường cao của ∆IBH nên ∆IBH là tam giác cân tại B có BE là đường trung trực của cạnh HI.
Vậy H và I đối xứng với nhau qua BC.
d) D, E lần lượt là giao của AO và AI với BC.
Do OK // EI nên theo định lí Ta-lét ta có:
\(\frac{{EI}}{{OK}} = \frac{{EG}}{{GK}} \Rightarrow \frac{{EH}}{{OK}} = \frac{{EG}}{{GK}}\).
Và \(\widehat {EIG} = \widehat {GOK}\) (Hai góc ở vị trí so le trong) (1)
Do OK // EA nên theo định lí Ta-lét ta có:
\(\frac{{OK}}{{AE}} = \frac{{DK}}{{DE}} \Rightarrow \frac{{AE}}{{OK}} = \frac{{DE}}{{DK}}\).
Và \(\widehat {DOK} = \widehat {DAE}\) (Hai góc ở vị trí đồng vị) (2)
Ta có:
\(\frac{{AH}}{{OK}} = \frac{{AE}}{{OK}} - \frac{{EH}}{{OK}} = \frac{{ED}}{{DK}} - \frac{{EG}}{{GK}}\) (*)
Tam giác OIA cân tại O do có OI = OA (3)
Từ (1), (2), (3) suy ra \(\widehat {GOK} = \widehat {DOK}\).
Þ OK là đường phân giác của tam giác DOG mà OK cũng là đường cao nên OK là đường trung trực của tam giác DOG cân tại O
Þ GK = DK
Khi đó (*) trở thành: \(\frac{{AH}}{{OK}} = \frac{{ED}}{{DK}} - \frac{{EG}}{{GK}} = \frac{{ED}}{{GK}} - \frac{{EG}}{{GK}} = \frac{{GD}}{{GK}} = 2\).
Vậy tỉ số \[\frac{{AH}}{{OK}}\] không đổi.
Do BC cố định nên ta luôn xây dựng được một đường tròn (J) là đường tròn ngoại tiếp của tam giác HBC. Vậy nên H luôn chuyển động trên một cung cố định.

