Trên đoạn thẳng AB lấy một điểm M (MA > MB). Trên cùng một nửa mặt phẳng có bờ AB

Đề bài. Trên đoạn thẳng AB lấy một điểm M (MA > MB). Trên cùng một nửa mặt phẳng có bờ AB, vẽ các tam giác đều AMC, BMD. Gọi E, F, I, K theo thứ tự là trung điểm của CM, CB, DM, DA. Chứng minh rằng EFIK là hình thang cân và $KF=\frac{1}{2}CD$

Trả lời

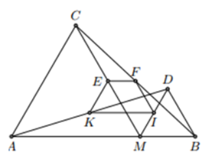Gọi EK giao AB tại P

Xét Δ CMB có EF là đường trung bình của Δ

⇒ EF // MB ⇒ EF // AB. (1)

Xét ΔΔADM có KI là đường trung bình của Δ

⇒ KI // AM ⇒⇒ KI // AB. (2)

Từ (1) và (2) ⇒ Tứ giác EFIK là hình thang (*)

Gọi P; Q lần lượt là trung điểm của AM và BN.

Xét Δ ACM có PE là đường trung bình của ΔΔ.

⇒ PE // AC mà AC // MD (Do $\widehat{A}=\widehat{M}={60}^{\circ }$ở vị trí đồng vị)

⇒ PE // MD (3)

Mặt khác ΔΔADM có PK là đường trung bình của ΔΔ.

⇒ PK // MD (4)

Từ (3) và (4) ⇒ P; E; K thẳng hàng mà PE // AC nên KE // AC (5).

Từ (2) và (5) ⇒ $\widehat{CAB}=\widehat{EKI}$ (Hai góc nhọn có cạnh tương ứng song song)

Mà $\widehat{CAB}={60}^{\circ }$(**)

Chứng minh tương tự ta được F; I; Q thẳng hàng mà QF // MC nên IF // MC;

Lại có MC // BD nên FI // BD (6).

Từ (2) và (6) ⇒ $\widehat{DBA}=\widehat{FIK}$ (Hai góc nhọn có cạnh tương ứng song song)

Mà $\widehat{DAB}={60}^{\circ }$

⇒ $\widehat{FIK}={60}^{\circ }$

Từ (*); (**) và (***)

⇒ EFIK là hình thang cân (Hình thang có 2 góc ở đáy bằng nhau là hình thang cân)

⇒ đcpm