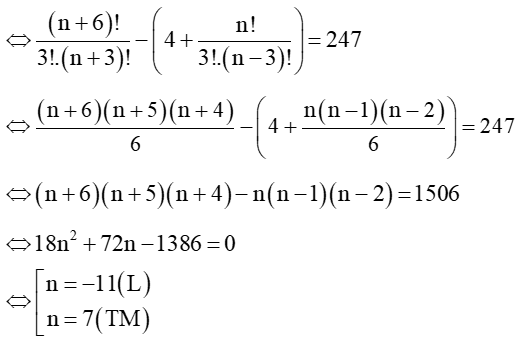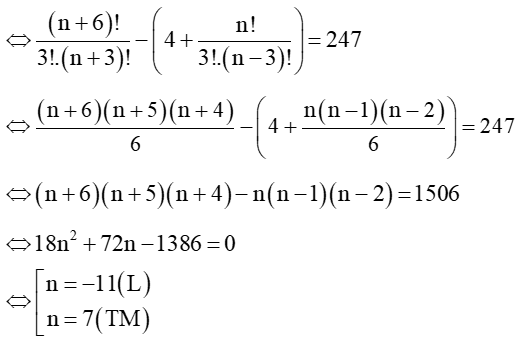Trên các cạnh AB, BC, CA của ∆ABC lần lượt lấy 2, 4, n (n > 3) điểm phân biệt
152
24/06/2023
Đề bài: Trên các cạnh AB, BC, CA của ∆ABC lần lượt lấy 2, 4, n (n > 3) điểm phân biệt (các điểm không trùng với các đỉnh của tam giác). Tìm n, biết rằng số tam giác có các đỉnh thuộc n + 6 điểm đã cho là 247.
Vậy n = 7.
Trả lời
Hướng dẫn giải:
Nhận xét: Mỗi tam giác được lập thành do một cách chọn 3 điểm sao cho 3 điểm đó không thẳng hàng tức là không cùng nằm trên một cạnh của ∆ABC.
Chọn ngẫu nhiên 3 điểm từ n + 6 điểm đã cho có: cách.
Chọn 3 điểm chỉ nằm trên đúng 1 cạnh của ∆ABC có: (cách).
Số tam giác lập thành là: