Tính thể tích V của khối chóp tam giác đều S.ABC, biết chiều cao hình chóp bằng h

Đề bài: Tính thể tích V của khối chóp tam giác đều S.ABC, biết chiều cao hình chóp bằng h, $\widehat{SBA}=\alpha$ .

Trả lời

Hướng dẫn giải:

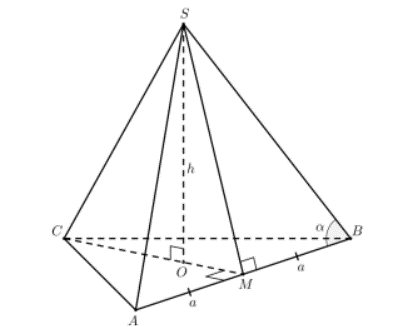
Gọi O là trọng tâm ∆ABC và M là trung điểm AB. Đặt AB = 2a (a > 0)

Vì O cũng là tâm đường trong ngoại tiếp ∆ABC nên SO ⊥ (ABC)

Mặt khác, vì ∆SAB cân tại S nên SM ⊥ AB

⇒ ∆SMB vuông tại M ⇒ SM = MB. tan𝛂 = atan𝛂 (1).

Ngoài ra, $OM=\frac{1}{3}CM=\frac{1}{3}.\frac{2a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}$

∆SOM vuông tại O ⇒ SM = $\sqrt{S{O}^2+O{M}^2}=\sqrt{h^2+\frac{a^2}{3}}\left(2\right)$

Từ (1) và (2) ⇒𝛂tan𝛂 = $\sqrt{h^2+\frac{a^2}{3}}\Rightarrow 3a^2.{\tan }^2\alpha =3h^2+a^2\Rightarrow a^2.(3{\tan }^2\alpha -1)=3h^2$

$\Rightarrow a^2=\frac{3h^2}{3{\tan }^2\alpha -1}\Rightarrow S_{ABC}=\frac{{\left(2a\right)}^2\sqrt{3}}{4}=a^2\sqrt{3}=\frac{3h^2\sqrt{3}}{3{\tan }^2\alpha -1}$

Vậy $V=\frac{1}{3}.SO.S_{ABC}=\frac{1}{3}.h.\frac{3h^2\sqrt{3}}{3{\tan }^2\alpha -1}=\frac{h^3\sqrt{3}}{3{\tan }^2\alpha -1}$ .