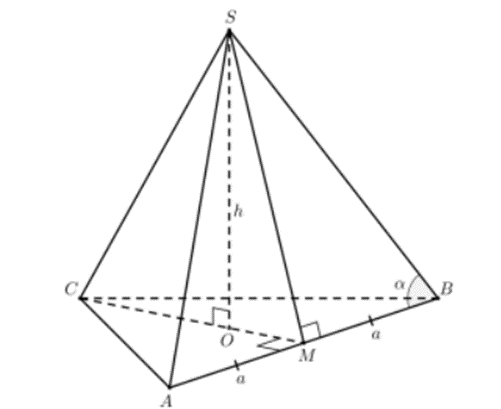
Gọi O là trọng tâm ∆ABC và M là trung điểm AB. Đặt AB = 2a (a > 0)

Vì O cũng là tâm đường trong ngoại tiếp ∆ABC nên SO ⊥ (ABC)

Mặt khác, vì ∆SAB cân tại S nên SM ⊥ AB

⇒ ∆SMB vuông tại M ⇒ SM = MB. tan𝛂 = atan𝛂 (1).

Ngoài ra, \(OM = \frac{1}{3}CM = \frac{1}{3}.\frac{{2a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\)

∆SOM vuông tại O ⇒ SM = \(\sqrt {S{O^2} + O{M^2}} = \sqrt {{h^2} + \frac{{{a^2}}}{3}} (2)\)

Từ (1) và (2) ⇒𝛂tan𝛂 = \(\sqrt {{h^2} + \frac{{{a^2}}}{3}} \Rightarrow 3{a^2}.{\tan ^2}\alpha = 3{h^2} + {a^2} \Rightarrow {a^2}.(3{\tan ^2}\alpha - 1) = 3{h^2}\)

\( \Rightarrow {a^2} = \frac{{3{h^2}}}{{3{{\tan }^2}\alpha - 1}} \Rightarrow {S_{ABC}} = \frac{{{{(2a)}^2}\sqrt 3 }}{4} = {a^2}\sqrt 3 = \frac{{3{h^2}\sqrt 3 }}{{3{{\tan }^2}\alpha - 1}}\)

Vậy \(V = \frac{1}{3}.SO.{S_{ABC}} = \frac{1}{3}.h.\frac{{3{h^2}\sqrt 3 }}{{3{{\tan }^2}\alpha - 1}} = \frac{{{h^3}\sqrt 3 }}{{3{{\tan }^2}\alpha - 1}}\).