Tính thể tích của khối lăng trụ ABC.A’B’C’ biết tất cả các cạnh bằng a và hình chiếu của A’ trên mặt phẳng (ABC) là trung điểm của AB

Luyện tập 4 trang 112 Toán 11 Tập 2: Tính thể tích của khối lăng trụ ABC.A’B’C’ biết tất cả các cạnh bằng a và hình chiếu của A’ trên mặt phẳng (ABC) là trung điểm của AB.

Trả lời

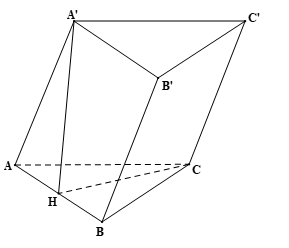
Gọi H là trung điểm của AB nên $AH=\frac{AB}{2}=\frac{a}{2}.$

Vì hình chiếu của A’ trên mặt phẳng (ABC) là trung điểm của AB nên A’H ⊥ (ABC).

Ta có: A’H ⊥ (ABC) và AB ⊂ (ABC) nên A’H ⊥ AB.

Áp dụng định lí Pythagore vào tam giác A’AH vuông tại H (do A’H ⊥ AB) có:

A’A² = A’H² + AH²

Do đó $A^{\text{'}}H=\sqrt{A^{\text{'}}{A}^2-A{H}^2}=\sqrt{a^2-{\left(\frac{a}{2}\right)}^2}=\sqrt{a^2-\frac{a^2}{4}}=\sqrt{\frac{3a^2}{4}}=\frac{a\sqrt{3}}{2}.$

Xét ∆ABC đều có: CH là đường trung tuyến (do H là trung điểm của AB) nên CH cũng là đường cao của tam giác ABC hay CH ⊥ AB.

Áp dụng định lí Pythagore vào tam giác ACH vuông tại H (do CH ⊥ AB) có:

AC² = AH² + CH²

Do đó $CH=\sqrt{A{C}^2-A{H}^2}=\sqrt{a^2-{\left(\frac{a}{2}\right)}^2}=\sqrt{a^2-\frac{a^2}{4}}=\sqrt{\frac{3a^2}{4}}=\frac{a\sqrt{3}}{2}.$

Khi đó, diện tích tam giác ABC có đường cao $CH=\frac{a\sqrt{3}}{2}$ là:

$S_{\Delta ABC}=\frac{1}{2}CH.AB=\frac{1}{2}.\frac{a\sqrt{3}}{2}.a=\frac{a^2\sqrt{3}}{4}$ (đvdt)

Thể tích của khối lăng trụ ABC.A’B’C’ có chiều cao $A^{\text{'}}H=\frac{a\sqrt{3}}{2}$ và diện tích đáy $S_{\Delta ABC}=\frac{a^2\sqrt{3}}{4}$ là:

$V_{ABC.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}=S_{\Delta ABC}.A^{\text{'}}H=\frac{a^2\sqrt{3}}{4}\cdot \frac{a\sqrt{3}}{2}=\frac{3a^3}{8} \left(đvtt\right)$

Xem thêm các bài giải SGK Toán lớp 11 Cánh diều hay, chi tiết khác: