Luyện tập 3 trang 111 Toán 11 Tập 2: Cho hình chóp đều S.ABC. Gọi A’, B’, C’ lần lượt là trung điểm của các đoạn thẳng SA, SB, SC. Chứng minh rằng phần hình chóp đã cho giới hạn bởi hai mặt phẳng (ABC) và (A’B’C’) là hình chóp cụt đều.
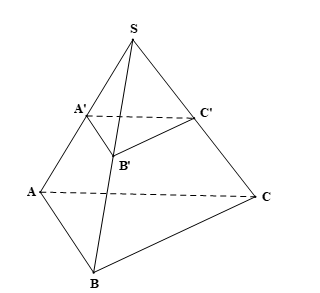
⦁ Xét ∆SAB có: A’, B’ lần lượt là trung điểm của SA, SB nên A’B’ là đường trung bình của ∆SAB. Do đó A’B’ // AB.
Mà AB ⊂ (ABC).
Suy ra A’B’ // (ABC).
⦁ Chứng minh tương tự, ta cũng có B’C’ // (ABC).
Ta có: A’B’ // (ABC), B’C’ // (ABC) và A’B’ ∩ B’C’ = B’ trong (A’B’C’).
Suy ra (A’B’C’) // (ABC).
Mà S.ABC là hình chóp đều.
Vậy phần hình chóp đã cho giới hạn bởi hai mặt phẳng (ABC) và (A’B’C’) là hình chóp cụt đều.
Xem thêm các bài giải SGK Toán lớp 11 Cánh diều hay, chi tiết khác: