Tìm tập xác định của các hàm số sau: a) y = căn của ( 15.x^2 + 8.x - 12 ); b) y = (x-1)/ căn của
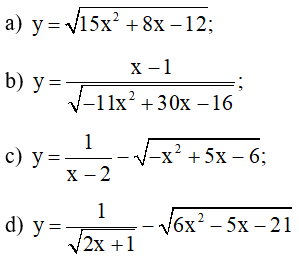
Bài 5 trang 14 SBT Toán 10 Tập 2: Tìm tập xác định của các hàm số sau:
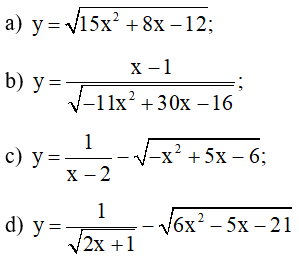
a) Hàm số xác định khi và chỉ khi 15x2 + 8x – 12 ≥ 0
Tam thức bậc hai f ( x ) = 15x2 + 8x – 12 có ∆ = 82 – 4.15. (–12) = 784 > 0 suy ra f(x) có hai nghiệm phân biệt x1 = và x2 =
Ta có: a = 15 > 0 nên f ( x ) ≥ 0 khi và chỉ khi x ≤ hoặc x ≥ .
Vậy tập xác định của hàm số là D = .
b) Hàm số xác định khi và chỉ khi –11x2 + 30x – 16 > 0
Tam thức bậc hai f ( x ) = –11x2 + 30x – 16 có ∆ = 302 – 4.( –11).( –16) = 196 > 0 suy ra f(x) có hai nghiệm phân biệt x1 = 2 và x2 =
Ta có: a = –11 < 0 nên f ( x ) > 0 khi và chỉ khi < x < 2.
Vậy tập xác định của hàm số là D =
c) Hàm số xác định khi và chỉ khi x – 2 ≠ 0 và –x2 + 5x – 6 ≥ 0.
+) Xét x – 2 ≠ 0 khi và chỉ khi x ≠ 2.
+) Xét tam thức bậc hai f ( x ) = –x2 + 5x – 6 có ∆ = 52 – 4.( –1).( –6) = 1 > 0 suy ra f(x) hai nghiệm phân biệt x1 = 3 và x2 = 2 ,
Ta có: a = –1 < 0 nên f ( x ) ≥ 0 khi và chỉ khi 2 ≤ x ≤ 3.
Suy ra hàm số xác định khi 2 < x ≤ 3.
Vậy tập xác định của hàm số là D = .
d) Hàm số xác định khi và chỉ khi 2x + 1 > 0 và 6x2 – 5x – 21 ≥ 0
+) Xét 2x + 1 > 0 khi và chỉ khi x >
+) Xét tam thức bậc hai f ( x ) = 6x2 – 5x – 21 có ∆ = (–5)2 – 4.6.( –21) = 529 > 0 suy ra f(x) hai nghiệm phân biệt x1 = và x2 =
Ta có a = 6 > 0 nên f ( x ) ≥ 0 khi và chỉ khi x ≤ hoặc x ≥ mà x > nên x ≥
Vậy tập xác định của hàm số là D = .
Xem thêm các bài giải SBT Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Dấu của tam thức bậc hai
Bài 2: Giải bất phương trình bậc hai một ẩn