Thiết kế của một chiếc cổng có hình parabol với chiều cao 5 m và khoảng cách giữa hai chân cổng là 4 m

Bài 12 trang 15 SBT Toán 10 Tập 2: Thiết kế của một chiếc cổng có hình parabol với chiều cao 5 m và khoảng cách giữa hai chân cổng là 4 m.

a) Chọn trục hoành là đường thẳng nối hai chân cổng, gốc toạ độ tại một chân cổng, chân cổng còn lại có hoành độ dương, đơn vị là 1 m. Hãy viết phương trình của vòm cổng.

b) Người ta cần chuyển một thùng hàng hình hộp chữ nhật với chiều cao 3 m. Chiều rộng của thùng hàng tối đa là bao nhiêu để thùng có thể chuyển lọt qua được cổng?

Lưu ý: Đáp số làm tròn đến hàng phần trăm.

Trả lời

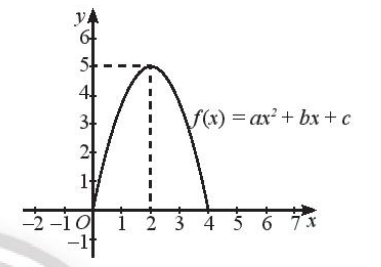
a) Đặt gốc tọa độ tại một chân cổng như hình vẽ trên.

Vì chiếc cổng có dạng parabol nên phương trình y = ax² + bx + c của đường viền cổng.

Do một chân cổng có tọa độ ( 0;0 ) nên ta có c = 0 (1).

Khoảng cách giữa hai chân cổng là 4 m nên chân cổng còn lại có tọa độ ( 4;0 ), ta có 16a + 4b + c = 0 (2)

Cổng có chiều cao 5 m nên tọa độ đỉnh cổng là ( 2; 5 ), ta có: 4a + 2b + c = 5 (3)

Thay (1) vào (2) và (3) ta được hệ phương trình:

 $\left\{\begin{array}{l}16\text{a}+4\text{b}=0\\ 4\text{a}+2\text{b}=5\end{array}\right.$

Từ đó suy ra a = –1,25; b = 5 và c = 0.

Vậy phương trình của vòm cổng là y = –1,25x² + 5x

b) Ta xác định các hoành độ x mà tại đó vòm cổng cao hơn thùng hàng bằng cách giải bất phương trình y = –1,25x² + 5x ≥ 3 hay –1,25x² + 5x – 3 ≥ 0.

Tam thức bậc hai f ( x ) = –1,25x² + 5x – 3 có ∆ = 5² – 4.(– 1,25).(– 3) = 10 > 0 nên f(x) có hai nghiệm phân biệt x₁ = 0,74 và x₂ = 3,26, a = –1,25 < 0 nên f ( x ) ≥ 0 khi và chỉ khi 0,74 ≤ x ≤ 3,26.

Vậy chiều rộng tối đa của thùng hàng là 3,26 – 0,74 = 2,52 m.

Xem thêm các bài giải SBT Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 6

Bài 1: Dấu của tam thức bậc hai

Bài 2: Giải bất phương trình bậc hai một ẩn

Bài 3: Phương trình quy về phương trình bậc hai

Bài tập cuối chương 7

Bài 1: Quy tắc cộng và quy tắc nhân