Tìm số tự nhiên n sao cho: n^2 ​+ 3n + 6 chia hết n + 3

Đề bài: Tìm số tự nhiên n sao cho: n² ​+ 3n + 6 chia hết n + 3

Trả lời

Hướng dẫn giải:

Ta có:

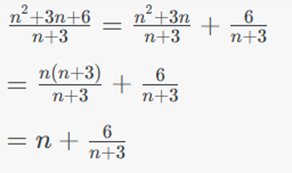
Để n² ​+ 3n + 6 chia hết n + 3 thì 6 chia hết cho n + 3

Suy ra n + 3 ∈ Ư(6) = { 1; 2; 3; 6; – 1 ; – 2; – 3– 6}

Với n + 3 = 1 thì n = – 2 (loại)

Với n + 3 = 2 thì n = – 1 (loại)

Với n + 3 = 3 thì n = 0 (thỏa mãn)

Với n + 3 = 6 thì n = 3 (thỏa mãn)

Với n + 3 = – 1 thì n = – 4 (loại)

Với n + 3 = – 2 thì n = – 5 (loại)

Với n + 3 = – 3 thì n = – 6 (loại)

Với n + 3 = – 6 thì n = – 9 (loại)

Vậy n = 0, n = 3.