Tìm số tự nhiên n để giá trị biểu thức sau là số nguyên tố: A = n^3 – 4n^2 + 4n – 1

Câu 25: Tìm số tự nhiên n để giá trị biểu thức sau là số nguyên tố: A = n³ – 4n² + 4n – 1.

Trả lời

Điều kiện: n ∈ ℕ.

Ta có A = n³ – 4n² + 4n – 1

= (n³ – 1) – (4n² – 4n)

= (n – 1)(n² + n + 1) – 4n(n – 1)

= (n – 1)(n² + n + 1 – 4n)

= (n – 1)(n² – 3n + 1).

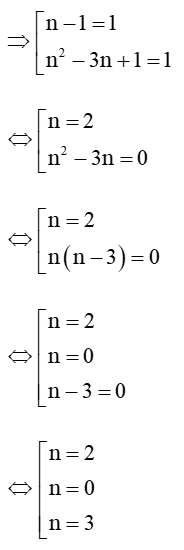
Để A là số nguyên tố thì A là tích của 1 và chính nó (A > 1).

Với n = 2, ta có: A = n³ – 4n² + 4n – 1 = 2³ – 4.2² + 4.2 – 1 = –1 < 1.

Do đó ta loại n = 2.

Với n = 0, ta có: A = n³ – 4n² + 4n – 1 = 0³ – 4.0² + 4.0 – 1 = –1 < 1.

Do đó ta loại n = 0.

Với n = 3, ta có: A = n³ – 4n² + 4n – 1 = 3³ – 4.3² + 4.3 – 1 = 2 > 1.

Do đó ta nhận n = 3.

So với điều kiện n ∈ ℕ, ta nhận n = 3.

Vậy n = 3 thỏa mãn yêu cầu bài toán.