Tìm m để phương trình sau có 3 nghiệm phân biệt.

x³ − 6x² + 3(m + 2)x − m − 6 = 0.

Lời giải

x³ − 6x² + 3(m + 2)x − m − 6 = 0

Û x³ − 6x² + 3mx + 6x − m − 6 = 0

Û x³ − 6x² + 6x − 6 = m(1 − 3x) (1)

• TH1: 1 − 3x = 0 \( \Leftrightarrow x = \frac{1}{3}\).

Khi đó, phương trình (*) trở thành \( - \frac{{125}}{{27}} = m.0\) (vô nghiệm).

• TH2: 1 ≠ 3x = 0 \( \Leftrightarrow x \ne \frac{1}{3}\) .

Khi đó, phương trình (1) trở thành \(m = \frac{{{x^3} - 6{x^2} + 6x - 6}}{{1 - 3x}} = f\left( x \right)\) (*)

Số nghiệm của phương trình (*) là số giao điểm của đồ thị hàm số y = f (x) và đường thẳng y = m.

Ta có:

\(f'\left( x \right) = \frac{{\left( {3{x^2} - 12x + 6} \right)\left( {1 - 3x} \right) + 3\left( {{x^3} - 6{x^2} + 6x - 6} \right)}}{{{{\left( {1 - 3x} \right)}^2}}}\)

\( \Rightarrow f'\left( x \right) = \frac{{ - 6{x^3} + 21{x^2} - 12x - 12}}{{{{\left( {1 - 3x} \right)}^2}}} = 0\)

\( \Rightarrow - 6{x^3} + 21{x^2} - 12x - 12 = 0\) 

Û 2x³ − 7x² + 4x + 4 = 0

Û (2x + 1)(x − 2)² = 0

\[ \Rightarrow \left[ \begin{array}{l}x = \frac{{ - 1}}{2}\\x = 2\end{array} \right.\].

Ta có BBT:

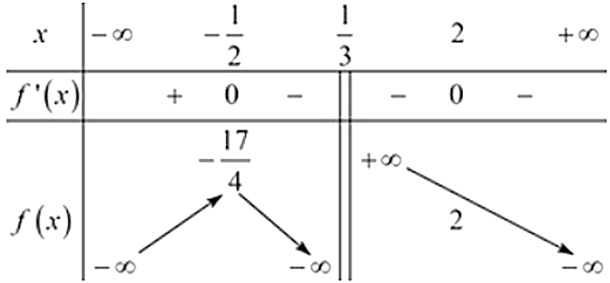
Dựa vào BBT ta thấy phương trình (*) có 2 nghiệm phân biệt khi và chỉ khi \(m = - \frac{{17}}{4}.\)