Tìm hai số tự nhiên, biết: a) Có tích bằng 720 và ƯCLN bằng 6. b) Có tích bằng 4050 và ƯCLN bằng 3
Câu 1: Tìm hai số tự nhiên, biết:
a) Có tích bằng 720 và ƯCLN bằng 6.
b) Có tích bằng 4050 và ƯCLN bằng 3.
a) Gọi hai số tự nhiên cần tìm là a, b.
Ta có ƯCLN(a, b) = 6.
Suy ra a = 6m; b = 6n và ƯCLN(m, n) = 1.
Lại có a.b = 720.
Suy ra 6m.6n = 720.
Do đó 36m.n = 720.
Vì vậy m.n = 20.
Chọn các cặp m, n nguyên tố cùng nhau và có tích bằng 20, ta được bảng sau:
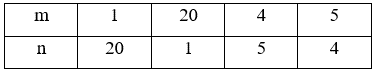
Khi đó ta có:
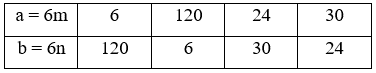
Vậy hai số tự nhiên cần tìm là 6; 120 hoặc 24; 30.
b) Gọi hai số tự nhiên cần tìm là a, b.
Ta có ƯCLN(a, b) = 3.
Suy ra a = 6m; b = 3n và ƯCLN(m, n) = 1.
Lại có a.b = 4050.
Suy ra 3m.3n = 4050.
Do đó 9m.n = 4050.
Vì vậy m.n = 450.
Chọn các cặp m, n nguyên tố cùng nhau và có tích bằng 450, ta được bảng sau:
Khi đó ta có:
Vậy hai số tự nhiên cần tìm là 3; 1350 hoặc 6; 675 hoặc 27; 150 hoặc 54; 75.