Tìm đa thức Q(x) sao cho P(x).Q(x) = R(x), biết: a) P(x) = x – 2, R(x) = –x^3 + 8
Bài 59 trang 56 SBT Toán 7 Tập 1:
Tìm đa thức Q(x) sao cho P(x).Q(x) = R(x), biết:
a) P(x) = x – 2, R(x) = –x3 + 8;
b) P(x) = x2 – 3x + 2, R(x) = 10 – 13x + 2x2 + x3.
Ta có P(x).Q(x) = R(x)
Suy ra Q(x) = R(x) : P(x).
a) Với P(x) = x – 2, R(x) = –x3 + 8 ta có:
Q(x) = (–x3 + 8) : (x – 2)
Ta thực hiện đặt tính chia đa thức như sau:
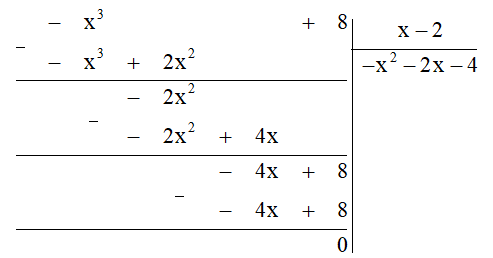
Khi đó Q(x) = (–x3 + 8) : (x – 2) = – x2 – 2x – 4.
Vậy Q(x) = – x2 – 2x – 4.
b) Với P(x) = x2 – 3x + 2, R(x) = 10 – 13x + 2x2 + x3 ta có:
Q(x) = (10 – 13x + 2x2 + x3) : (x2 – 3x + 2)
= (x3 + 2x2 – 13x + 10) : (x2 – 3x + 2)
Ta thực hiện đặt tính chia đa thức như sau:
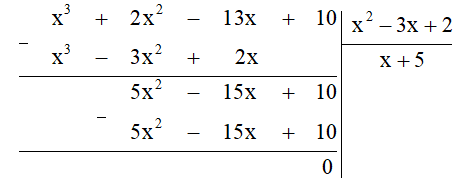
Khi đó Q(x) = (x3 + 2x2 – 13x + 10) : (x2 – 3x + 2) = x + 5.
Vậy Q(x) = x + 5.
Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 4. Phép nhân đa thức một biến
Bài 5. Phép chia đa thức một biến
Bài 1. Tổng các góc của một tam giác
Bài 2. Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác