tam giác ABD là tam giác đều và có cạnh bằng 2a. Tính thể tích của khối tứ diện ABCD
63
03/05/2024
Cho tứ diện ABCD có ABC là tam giác vuông cân tại C và nằm trong mặt phẳng vuông góc với mặt phẳng (ABD), tam giác ABD là tam giác đều và có cạnh bằng 2a. Tính thể tích của khối tứ diện ABCD
A. a3√33.
B. a3√3.
C. a3√39.
D. a3√2.
Trả lời
Chọn A
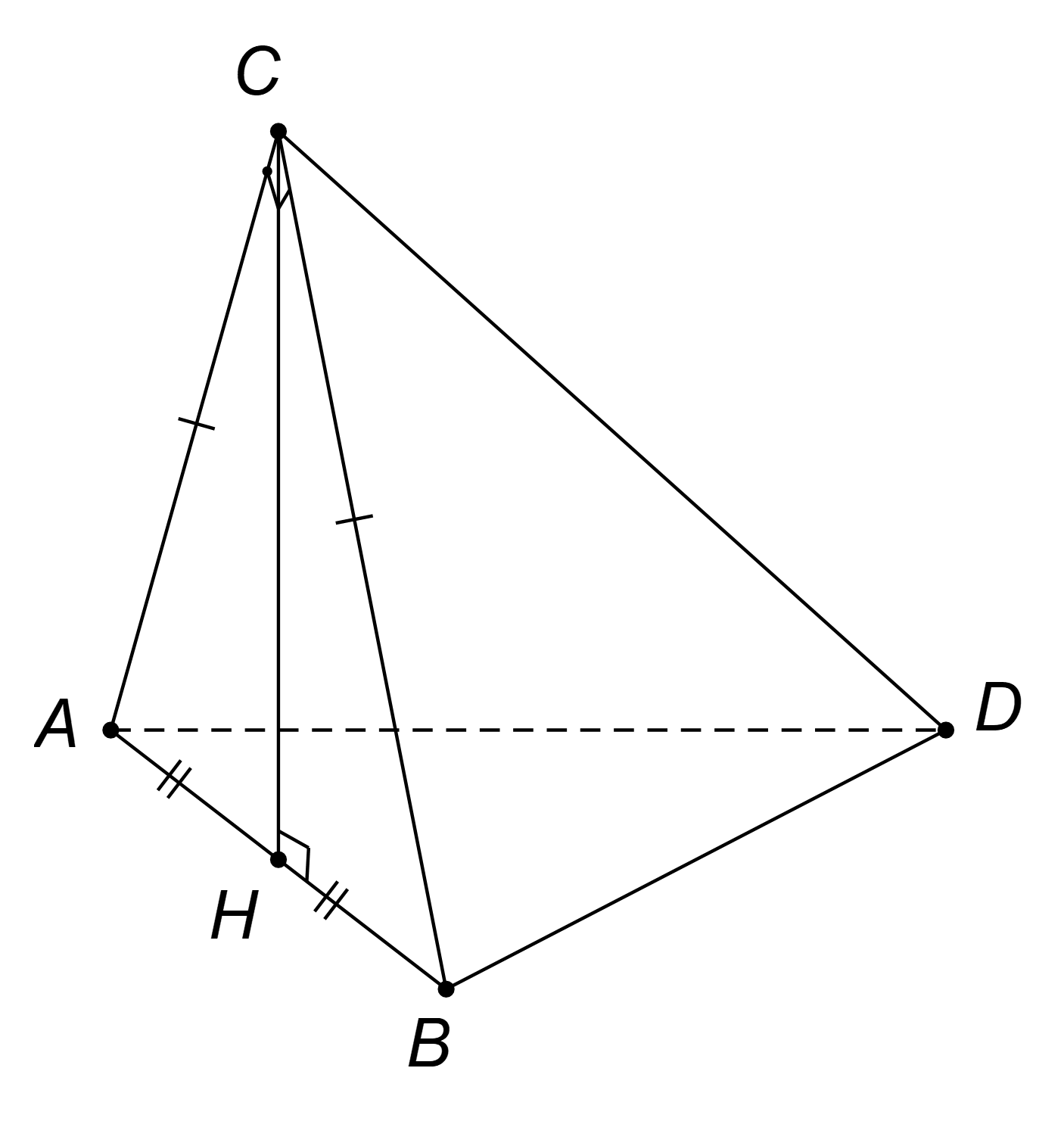
Gọi H là trung điểm của AB. Do đó,
CH⊥AB.Vì ABC là tam giác vuông cân tại C và nằm trong mặt phẳng vuông góc với mặt phẳng (ABD) nên
CH⊥(ABD).Xét tam giác ABC vuông cân tại C có CH là đường trung tuyến ứng với cạnh huyền AB nên
CH=12AB=12.2a=aVì tam giác ABD là tam giác đều và có cạnh bằng 2a nên
SΔABD=√34.(2a)2=a2.√3
Do đó, thể tích của khối tứ diện ABCD là: VABCD=13.CH.SΔABD=13a.a2.√3=a3√33.
