Cho hình chóp $S.ABC$ có các cạnh $AB=a$, $AC=a\sqrt{3}$, $SB>2a$ và góc $\angle ABC=\angle BAS=\angle BCS={90}^0$. Biết sin của góc giữa đường thẳng SB và mặt phẳng $\left(SAC\right)$ bằng $\frac{\sqrt{11}}{11}$. Tính thể tích khối chóp S.ABC

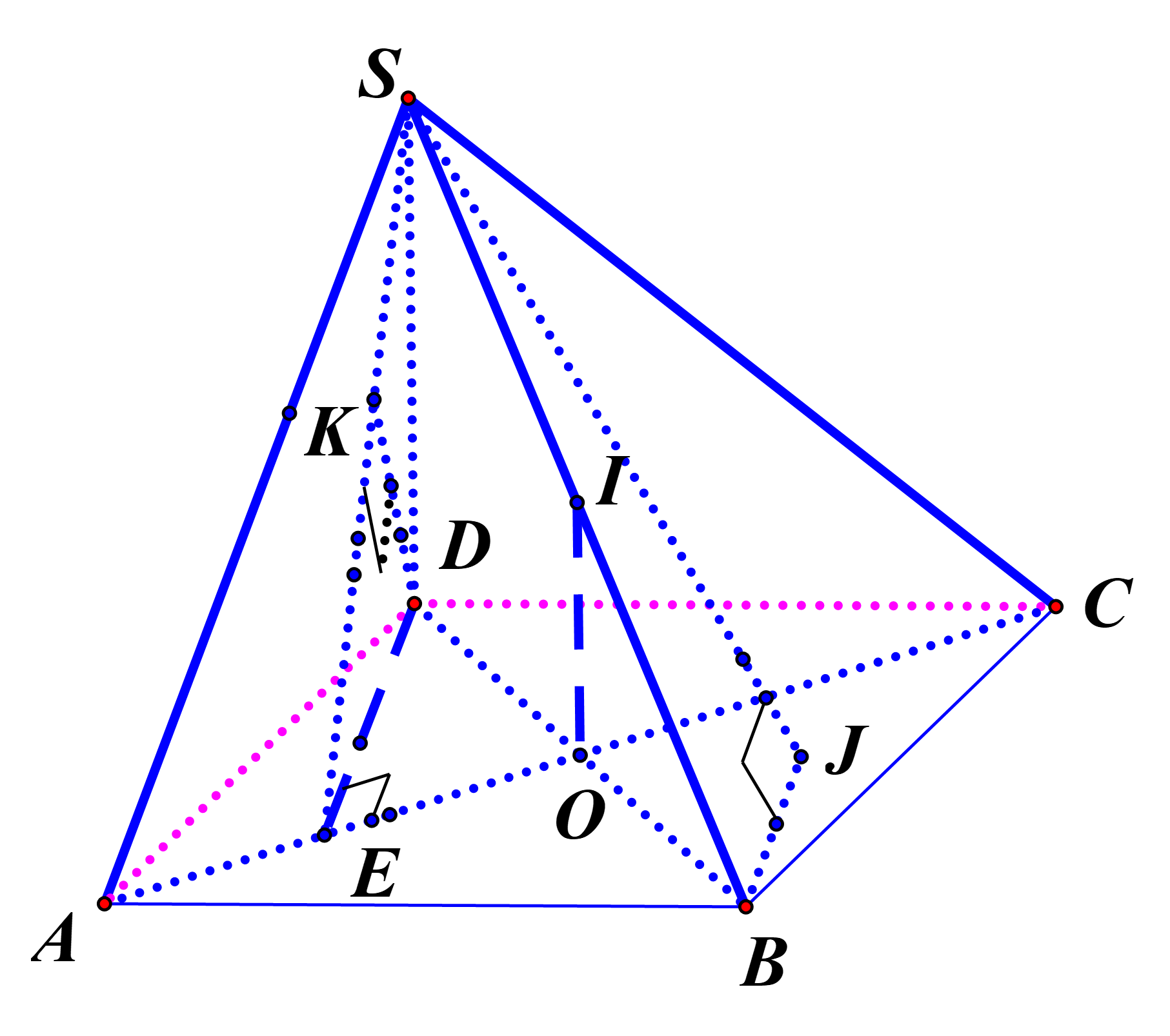
Gọi I là trung điểm SB, ta có $IA=IB=IC(=IS)$. Gọi O là trung điểm AC, vì tam giác ABCvuông tại B nên O là tâm đường tròn ngoại tiếp tam giác ABC. Suy ra $IO\perp \left(ABC\right)$
Gọi D là điểm đối xứng của B qua O, khi đó  $IO\parallel SD$ nên $SD\perp \left(ABCD\right)$. Đặt $SD=h$. Hạ $DE\perp AC,DK\perp SE$, khi đó $DK=d(D,(SAC\left)\right)$. Ta có
$\frac{1}{D{K}^2}=\frac{1}{S{D}^2}+\frac{1}{D{A}^2}+\frac{1}{D{C}^2}\Rightarrow D{K}^2=\frac{2a^2{h}^2}{2a^2+3h^2}$
Hạ $BJ\perp \left(SAC\right)$ suy ra góc giữa đường thẳng SB và mặt phẳng (SAC)
là góc $\angle BSJ$ . Ta có $\sin \angle BSJ=\frac{BJ}{SB}=\frac{\sqrt{11}}{11}\iff \frac{B{J}^2}{S{B}^2}=\frac{1}{11}\iff \frac{B{J}^2}{h^2+3a^2}=\frac{1}{11}\Rightarrow B{J}^2=\frac{h^2+3a^2}{11}$
Ta thấy $d(D,(SAC\left)\right)=d(B,(SAC\left)\right)\Rightarrow DK=BJ$. Do đó
$\frac{2a^2{h}^2}{2a^2+3h^2}=\frac{h^2+3a^2}{11}\iff \left(h^2+3a^2\right)\left(2a^2+3h^2\right)=22a^2{h}^2$
$\iff 3h^4-11a^2{h}^2+6a^4=0$$\iff h^2=3a^2$hoặc  $h^2=\frac{2}{3}{a}^2$
Trong tam giác vuông SBD có $SB>2a$,$BD=a\sqrt{3}$ nên $SD>a$, hay $h>a$. Suy ra $h=a\sqrt{3}$.Vậy $V_{S.ABC}=\frac{1}{3}SD.S_{ABC}=\frac{1}{3}a\sqrt{3}\left(\frac{1}{2}a.a\sqrt{2}\right)=\frac{a^3\sqrt{6}}{6}$