Tam giác ABC có AB = 3; AC = 6 và góc A = 60°. Tính bán kính của đường tròn ngoại tiếp tam giác ABC. A. 2; B. 3; C. 5; D. 6.
123
25/11/2023
Câu 33: Tam giác ABC có AB = 3; AC = 6 và góc A = 60°. Tính bán kính của đường tròn ngoại tiếp tam giác ABC.
A. 2;
B. 3;
C. 5;
D. 6.
Trả lời
Đáp án đúng là: B
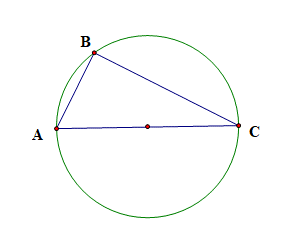
Áp dụng định lí Cosin, ta có
BC2 = AB2 + AC2 – 2AB . AC . cosA = 32 + 62 – 2 . 3 . 6 . cos60° = 27
Ta thấy: BC2 + AB2 = 27 + 9 = 36 = 62 = AC2
Suy ra tam giác ABC vuông tại B
Do đó bán kính đường tròn ngoại tiếp tam giác ABC là
R = AC : 2 = 3
Vậy ta chọn đáp án B.

