Quan sát Hình 15 và giải thích vì sao: Hai góc xOy và yOz là hai góc kề bù

Hoạt động 6 trang 94 Toán lớp 7 Tập 1: Quan sát Hình 15 và giải thích vì sao:

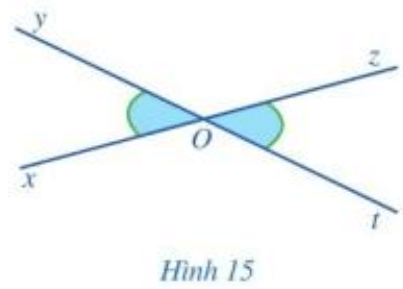
a) Hai góc xOy và yOz là hai góc kề bù;

b) Hai góc yOz và zOt là hai góc kề bù;

c) $\widehat{xOy}+\widehat{yOz}=\widehat{yOz}+\widehat{zOt}$ và $\widehat{xOy}=\widehat{zOt}$.

Trả lời

a) Góc xOy có đỉnh là O và hai cạnh là Ox; Oy.

Góc yOz có đỉnh là O và hai cạnh là Oy; Oz.

Mặt khác: Ox; Oz nằm về hai phía so với đường thẳng chứa Oy

Nên hai góc xOy và yOz kề nhau (1)

Suy ra $\widehat{xOz}=\widehat{xOy}+\widehat{yOz}$.

Mà $\widehat{xOz}={180}^o$(do hình vẽ xz là một đường thẳng) nên $\widehat{xOy}+\widehat{yOz}={180}^o$.

Do đó, hai góc xOy và yOz bù nhau (2)

Từ (1) và (2) suy ra: Hai góc xOy và yOz là hai góc kề bù.

b) Góc yOz có đỉnh là O và hai cạnh là Oz; Oy.

Góc zOt có đỉnh là O và hai cạnh là Ot; Oz.

Mặt khác: Oy; Ot nằm về hai phía so với đường thẳng chứa Oz

Nên hai góc yOz và zOt kề nhau (3)

Suy ra $\widehat{yOt}=\widehat{yOz}+\widehat{zOt}$.

Mà $\widehat{yOt}={180}^o$ (do hình vẽ yt là một đường thẳng) nên $\widehat{yOz}+\widehat{zOt}={180}^o$.

Do đó, hai góc yOz và zOt bù nhau (4)

Từ (3) và (4) suy ra: Hai góc yOz và zOt là hai góc kề bù.

c) Vì $\widehat{xOy}+\widehat{yOz}={180}^o$ và $\widehat{yOz}+\widehat{zOt}={180}^o$.

Nên $\widehat{xOy}+\widehat{yOz}=\widehat{yOz}+\widehat{zOt}$.

Suy ra $\widehat{xOy}+\widehat{yOz}-\widehat{yOz}=\widehat{yOz}+\widehat{zOt}-\widehat{yOz}$ (ta trừ cả hai vế cho $\widehat{yOz}$)

Do đó $\widehat{xOy}=\widehat{zOt}$.

Vậy $\widehat{xOy}+\widehat{yOz}=\widehat{yOz}+\widehat{zOt}$ và $\widehat{xOy}=\widehat{zOt}$.

Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài 2: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác

Bài tập cuối chương 3

Bài 1: Góc ở vị trí đặc biệt

Bài 2: Tia phân giác của một góc

Bài 3: Hai đường thẳng song song

Bài 4: Định lí