Một trang trại cần thuê xe vận chuyển 450 con lợn và 35 tấn cám. Nơi cho thuê xe chỉ có 12 xe lớn và 10 xe nhỏ. Một chiếc xe lớn có thể chở 50 con lợn và 5 tấn cám. Một chiếc xe nhỏ có thể ch

Trả lời

Lời giải

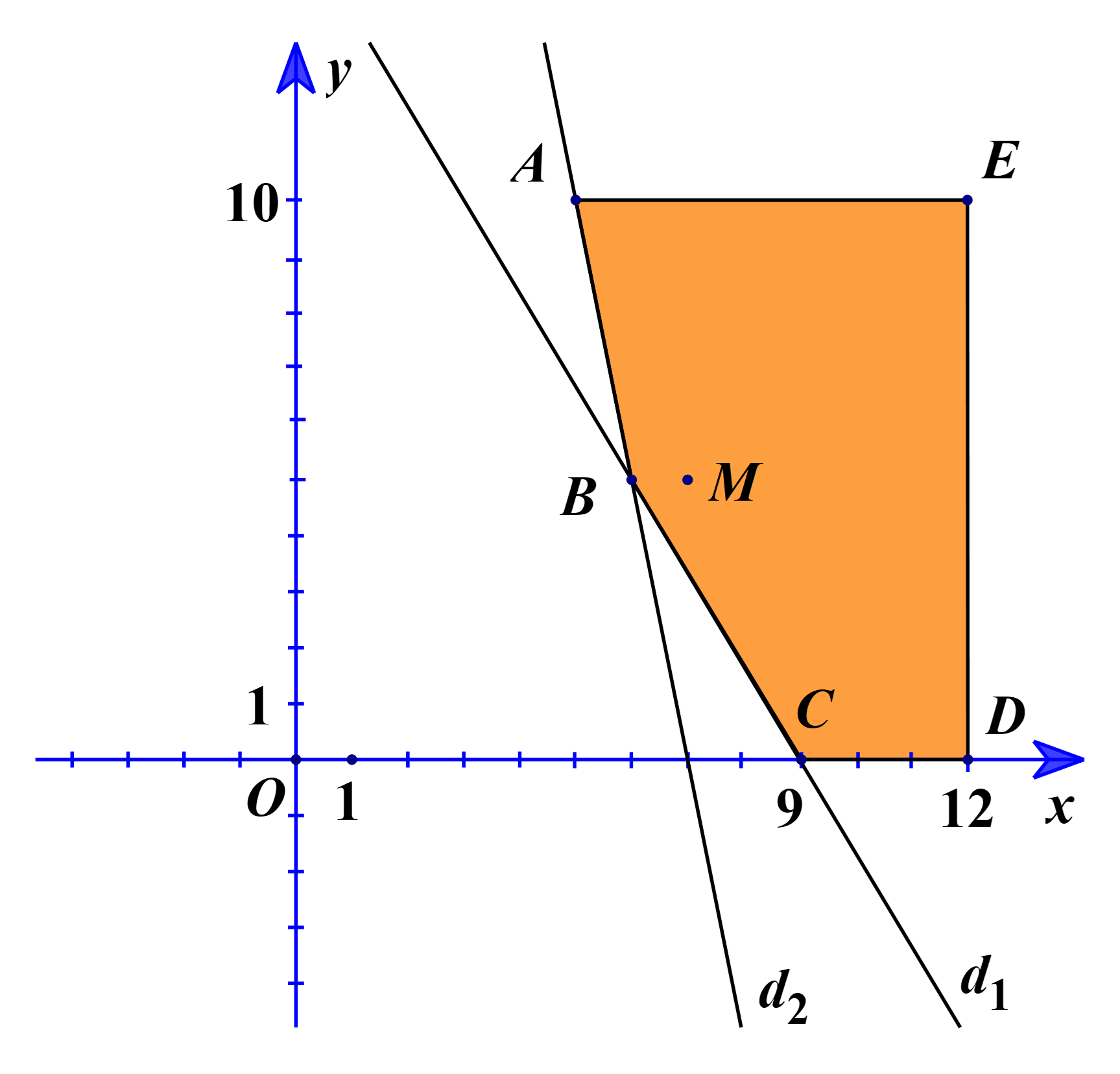
Gọi x, y (xe) lần lượt là số xe loại lớn, số xe loại nhỏ cần thuê (x, y ≥ 0, x, y ∈ ℤ).

Suy ra T = 4x + 2y (triệu đồng) là số tiền thuê xe.

Do đó yêu cầu bài toán ⇔ T nhỏ nhất.

Theo đề, ta có hệ: \(\left\{ \begin{array}{l}0 \le x \le 12\\0 \le y \le 10\\50x + 30y \ge 450\\5x + y \ge 35\end{array} \right.\)   (*)

Vẽ các đường thẳng d₁: 50x + 30y = 450 và d₂: 5x + y = 35 trên cùng một hệ trục tọa độ.

Tiếp theo, ta lấy điểm M(7; 5). Khi đó ta có: \(\left\{ \begin{array}{l}0 \le 7 \le 12\\0 \le 5 \le 10\\50.7 + 30.5 \ge 450\\5.7 + 5 \ge 35\end{array} \right.\) (đúng).

Suy ra miền nghiệm của hệ (*) là phần ngũ giác ABCDE, kể cả các đoạn thẳng AB, BC, CD, DE, EA, với A(5; 10), B(6; 5), C(9; 0), D(12; 0), E(12; 10).

Ta có T_A = 40, T_B = 34, T_C = 36, T_D = 48, T_E = 68.

Do đó T nhỏ nhất ⇔ x = 6, y = 5.

Vậy trang trại phải thuê 6 xe lớn, 5 xe nhỏ để chi phí thuê xe là thấp nhất.