Một nguồn phát sóng dao động điều hòa tạo ra sóng tròn đồng tâm O truyền
39
02/06/2024
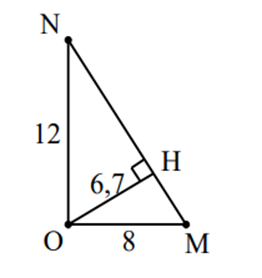
Một nguồn phát sóng dao động điều hòa tạo ra sóng tròn đồng tâm O truyền trên mặt nước với bước sóng λ. Hai điểm M và N thuộc mặt nước, nằm trên hai phương truyền sóng mà các phần tử nước đang dao động. Biết OM=8λ,ON=12λ và OM vuông góc với ON. Trên đoạn MN, số điểm mà phần tử nước dao động ngược pha với dao động của nguồn O là
A. 5.
B. 7.
C. 4.
D. 6.
Trả lời
+ Kẻ OH vuông góc với MN áp dụng hệ thức trong tam giác vuông có:
1OH2=1OM2+1ON2=1(8λ)2+1(12λ)2⇒OH≈6,7λ
+ Dễ thấy: Một điểm bất kì thuộc MN dao động ngược pha với nguồn O thỏa mãn điều kiện khoảng cách tới nguồn O bằng số bán nguyên lần bước sóng.
+ Trên MH có 1 điểm ngược pha với O có d=7,5λ
+ Trên NH có các điểm ngược pha với nguồn có khoảng cách lần lượt d=7,5λ;8,5λ;9,5λ;10,5λ;11,5λ; Có tổng cộng 5 điểm trên NH ngược pha với nguồn.
+ Vậy trên MN có 5 + 1 = 6 điểm ngược pha với nguồn O. Chọn đáp án D.