Khi thể tích khối tứ diện ABCD lớn nhất thì khoảng cách giữa hai đường thẳng AD và BC bằng.

28 03/05/2024

Cho tứ diện ABCD có

A B = A C = B D = C D = 1.

A. $\frac{1}{3} .$

B. $\frac{1}{\sqrt{3}} .$

C. $\frac{2}{\sqrt{3}} .$

D. $\frac{1}{\sqrt{2}} .$

Trả lời

Chọn B

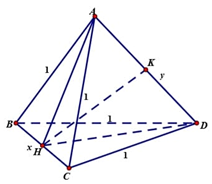
Đặt

B C = x; A D = y (x, y > 0) .

Gọi H, K lần lượt là trung điểm BC và AD

Δ A B C

cân tại A và

Δ D B C

cân tại

D \Rightarrow A H ⊥ B C, D H ⊥ B C \Rightarrow B C ⊥ (A H D) \Rightarrow B C ⊥ H K .

Mặt khác,

A H = D H \Rightarrow Δ H A D

cân tại

H \Rightarrow A D ⊥ H K .

Suy ra,

d (B C, A D) = H K .

Ta có:

A H = \sqrt{A B^{2} - B H^{2}} = \sqrt{1 - \frac{x^{2}}{4}} = \frac{\sqrt{4 - x^{2}}}{2} \Rightarrow H K = \sqrt{A H^{2} - A K^{2}} = \frac{\sqrt{4 - x^{2} - y^{2}}}{2} .

V_{A B C D} = \frac{1}{3} B C . S_{A H D} = \frac{1}{3} . B C . \frac{1}{2} . H K . A D = \frac{1}{12} x y \sqrt{4 - x^{2} - y^{2}}

Áp dụng bất đắng thức Cauchy ta có:

V_{A B C D} = \frac{1}{12} x y \sqrt{4 - x^{2} - y^{2}} = \frac{1}{12} \sqrt{x^{2} y^{2} (4 - x^{2} - y^{2})} \leq \frac{1}{12} \sqrt{{(\frac{x^{2} + y^{2} + 4 - x^{2} - y^{2}}{3})}^{3}} = \frac{2 \sqrt{3}}{27} .

Dấu = xảy ra

\Leftrightarrow x^{2} = y^{2} = 4 - x^{2} - y^{2} \Leftrightarrow x = y = \frac{2}{\sqrt{3}}

Do đó:

V_{\max} = \frac{2 \sqrt{3}}{27} \Leftrightarrow x = y = \frac{2}{\sqrt{3}} .

Khi đó:

H K = \frac{1}{\sqrt{3}} .

Bộ 20 đề thi giữa kì 2 Toán 12 có đáp án năm 2022-2023

Câu hỏi cùng chủ đề

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại B và C. Hai mặt phẳng

Bộ 20 đề thi giữa kì 2 Toán 12 có đáp án năm 2022-2023

66 6 tháng trước

Cho hàm số y=2-2/x-1 có đồ thị (C) và điểm M(3;-1). Gọi D là tập hợp tất cả các đường thẳng đi qua điểm

Bộ 20 đề thi giữa kì 2 Toán 12 có đáp án năm 2022-2023

72 6 tháng trước

Biết điểm M (xM, yM) thuộc đồ thị (C): 2x-2/x+1 sao cho khoảng cách từ M đến đường thẳng

Bộ 20 đề thi giữa kì 2 Toán 12 có đáp án năm 2022-2023

77 6 tháng trước

Cho hình chóp S.ABC có các cạnh AB=a,AC = a căn 3 ,SB>2a

Bộ 20 đề thi giữa kì 2 Toán 12 có đáp án năm 2022-2023

79 6 tháng trước

Cho hai tam giác đều ABC và ABD có độ dài cạnh bằng 1 và nằm trong hai mặt phẳng vuông góc

Bộ 20 đề thi giữa kì 2 Toán 12 có đáp án năm 2022-2023

63 6 tháng trước

Hàm số g(X)=f(X)-x^3/3+x^2-x+2 có bao nhiêu điểm cực đại?

Bộ 20 đề thi giữa kì 2 Toán 12 có đáp án năm 2022-2023

81 6 tháng trước

Cho hàm số y=2x-1/x+1 có đồ thị (C) và đường thẳng d:y=-x+m

Bộ 20 đề thi giữa kì 2 Toán 12 có đáp án năm 2022-2023

76 6 tháng trước

Gọi S là tập hợp các giá trị của tham số m để giá trị nhỏ nhất của hàm số y=(x^2+x+m)^2

Bộ 20 đề thi giữa kì 2 Toán 12 có đáp án năm 2022-2023

76 6 tháng trước

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA=a và SA vuông góc

Bộ 20 đề thi giữa kì 2 Toán 12 có đáp án năm 2022-2023

63 6 tháng trước

Gọi A,B,C là các điểm cực trị của đồ thị hàm số y=x^4-2x^2+4. Bán kính đường tròn

Bộ 20 đề thi giữa kì 2 Toán 12 có đáp án năm 2022-2023

89 6 tháng trước

Xem tất cả

Khi thể tích khối tứ diện ABCD lớn nhất thì khoảng cách giữa hai đường thẳng AD và BC bằng.

Trả lời

Câu hỏi cùng chủ đề

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại B và C. Hai mặt phẳng

Cho hàm số y=2-2/x-1 có đồ thị (C) và điểm M(3;-1). Gọi D là tập hợp tất cả các đường thẳng đi qua điểm

Biết điểm M (xM, yM) thuộc đồ thị (C): 2x-2/x+1 sao cho khoảng cách từ M đến đường thẳng

Cho hình chóp S.ABC có các cạnh AB=a,AC = a căn 3 ,SB>2a

Cho hai tam giác đều ABC và ABD có độ dài cạnh bằng 1 và nằm trong hai mặt phẳng vuông góc

Hàm số g(X)=f(X)-x^3/3+x^2-x+2 có bao nhiêu điểm cực đại?

Cho hàm số y=2x-1/x+1 có đồ thị (C) và đường thẳng d:y=-x+m

Gọi S là tập hợp các giá trị của tham số m để giá trị nhỏ nhất của hàm số y=(x^2+x+m)^2

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA=a và SA vuông góc

Gọi A,B,C là các điểm cực trị của đồ thị hàm số y=x^4-2x^2+4. Bán kính đường tròn

Danh mục