ho tam giác ABC vuông cân tại A. Qua A kẻ đường thẳng d bất kì sao cho đường thẳng d không cắt đoạn thẳng BC

Bài 5 trang 88 SBT Toán 8 Tập 1: Cho tam giác $ABC$ vuông cân tại $A$. Qua $A$ kẻ đường thẳng $d$ bất kì sao cho đường thẳng $d$ không cắt đoạn thẳng $BC$. Gọi $D,E$ lần lượt là hình chiếu của $B,C$ trên đường thẳng $d$. Chứng minh $A{D}^2+A{E}^2$ không phụ thuộc vào vị trí của đường thẳng $d$.

Trả lời

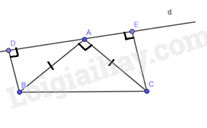
Ta chứng minh được:

$\widehat{BAD}+\widehat{ABD}={90}^{\circ }$ và $\widehat{BAD}+\widehat{CAE}={90}^{\circ }$ nên $\widehat{ABD}=\widehat{CAE}$.

$\mathrm{\Delta }ABD=\mathrm{\Delta }CAE$ (cạnh huyền – góc nhọn)

Suy ra $AD=CE$

Do đó $A{D}^2+A{E}^2=C{E}^2+A{E}^2=A{C}^2$ (vì tam giác $CAE$ vuông tại $E$)

Vậy $A{D}^2+A{E}^2$ không phụ thuộc vào vị trí của đường thẳng $d$.

Xem thêm các bài giải SBT Toán 8 Cánh diều hay, chi tiết khác:

Bài 2: Hình chóp tứ giác đều

Bài tập cuối chương 4 trang 78

Bài 1: Định lí Pythagore

Bài 2: Tứ giác

Bài 3: Hình thang cân

Bài 4: Hình bình hành