Hình thang vuông ABCD có góc A = góc D = 90 độ, AB = AD = 2 cm, DC = 4 cm
Hình thang vuông ABCD có \(\widehat A = \widehat D = 90^\circ ,\)AB = AD = 2 cm, DC = 4 cm. Tính các góc của hình thang ?
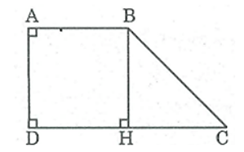
Kẻ BH ⊥ CD
Ta có: AD ⊥ CD (Vì ABCD là hình thang vuông có \(\widehat A = \widehat D = 90^\circ \)) ⇒ BH // AD
Hình thang ABHD có 2 cạnh bên song song nê HD = AB và BH = AD
AB = AD = 2 cm (gt) ⇒ BH = HD = 2 cm
CH = CD – HD = 4 - 2 = 2 (cm)
⇒ ∆BHC vuông cân tại H
Do đó, \(\widehat {HBC} = \widehat C\)
Lại có: \(\widehat {HBC} = \widehat C\) = 90° (tính chất tam giác vuông) \( \Rightarrow \widehat C = 45^\circ \)
\(\widehat B + \widehat C = 180^\circ \)( 2 góc trong cùng phía bù nhau) \( \Rightarrow \widehat B = 180^\circ - 45^\circ = 135^\circ \).