Hình chóp S.ABCD có đáy là hình thoi, AB = 2a, góc BAD = 120^0. Hình chiếu vuông góc của S lên (ABCD) là I, với I là giao điểm của hai đường chéo AC và BD, biết SI = a/2. Tính thể tích khối c
26
18/05/2024
Hình chóp S.ABCD có đáy là hình thoi, AB = 2a, \(\widehat {BAD} = 120^\circ \). Hình chiếu vuông góc của S lên (ABCD) là I, với I là giao điểm của hai đường chéo AC và BD, biết \(SI = \frac{a}{2}\). Tính thể tích khối chóp S. ABCD.
Trả lời
Lời giải
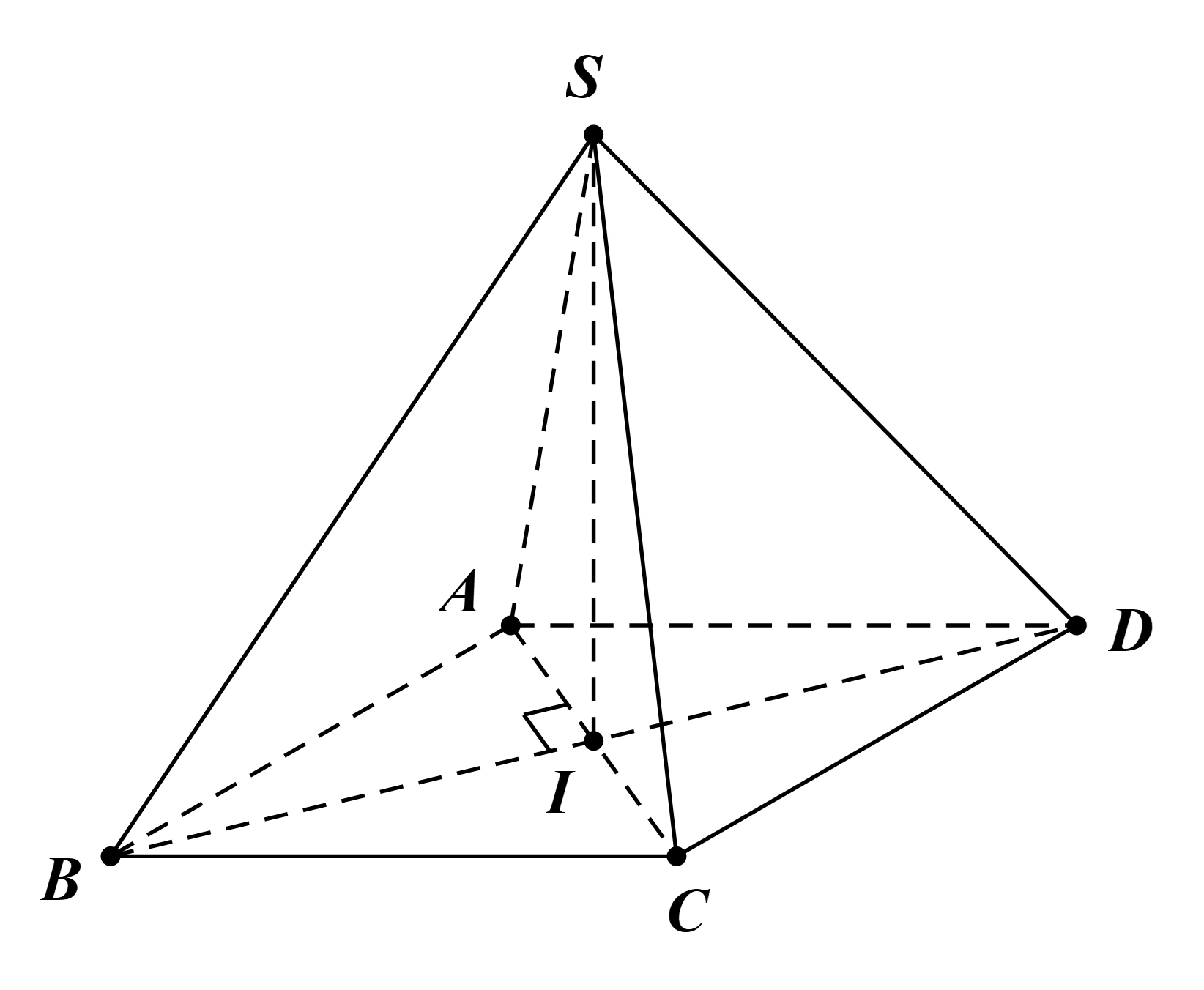
Tam giác AIB vuông tại I: \(\widehat {IAB} = \frac{{\widehat {BAD}}}{2} = \frac{{120^\circ }}{2} = 60^\circ \) (vì AC là tia phân giác của \(\widehat {BAD}\)).
Suy ra \(AI = AB\cos \widehat {IAB} = 2a.\cos 60^\circ = a\) và \(IB = AB.\sin \widehat {IAB} = 2a.\sin 60^\circ = a\sqrt 3 \).
Do đó AC = 2AI = 2a và \(BD = 2IB = 2a\sqrt 3 \).
Vậy thể tích của khối chóp S.ABCD là:
\({V_{S.ABCD}} = \frac{1}{3}.d\left( {S,\left( {ABCD} \right)} \right).{S_{ABCD}} = \frac{1}{3}.SI.\frac{1}{2}AC.BD = \frac{1}{6}.\frac{a}{2}.2a.2a\sqrt 3 = \frac{{{a^3}\sqrt 3 }}{3}\).

