Hàm số nghịch biến trên khoảng (pi; 2pi) là: A. y = sinx. B. y = cosx. C. y = tanx. D. y = cotx
Hàm số nghịch biến trên khoảng (π; 2π) là:
A. y = sinx.
B. y = cosx.
C. y = tanx.
D. y = cotx.
Hàm số nghịch biến trên khoảng (π; 2π) là:
A. y = sinx.
B. y = cosx.
C. y = tanx.
D. y = cotx.
Đáp án đúng là: D
Cách 1. Dùng đồ thị hàm số:
Xét đồ thị hàm số y = sinx:
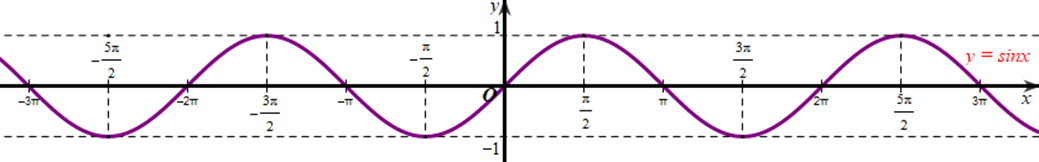
Xét đồ thị hàm số y = cosx:

Xét đồ thị hàm số y = tanx:
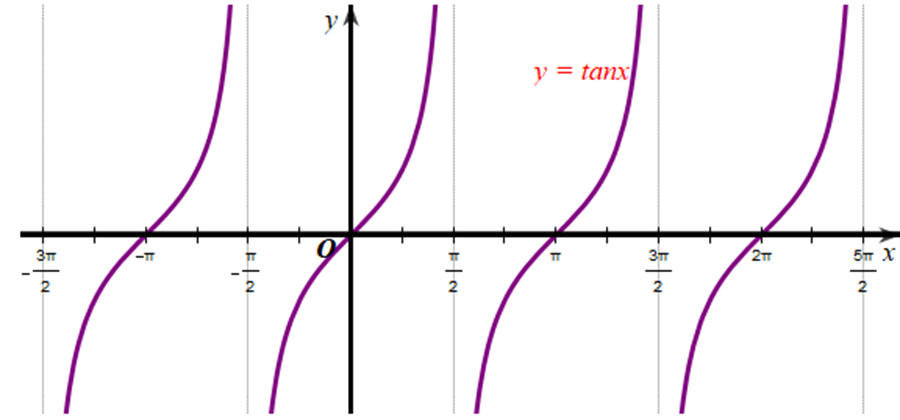
Xét đồ thị hàm số y = cotx:
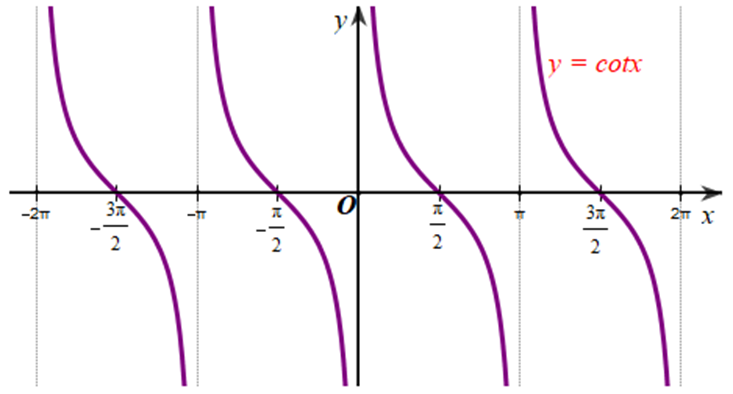
Quan sát các đồ thị trên, ta thấy hàm số y = cotx nghịch biến trên khoảng (π; 2π).
Cách 2. Dùng tính chất của hàm số lượng giác:
Do (π; 2π) = (0 + π; π + π)
Mà hàm số y = cotx nghịch biến trên mỗi khoảng (kπ; π + kπ) với k ∈ ℤ.
Do đó hàm số y = cotx nghịch biến trên khoảng (π; 2π).