Câu hỏi:
18/12/2023 200
Hai người cùng kéo một con thuyền với hai lực →F1=→OA,→F2=→OB có độ lớn lần lượt là 550 N, 800 N. Cho biết góc giữa hai vectơ là 52o.
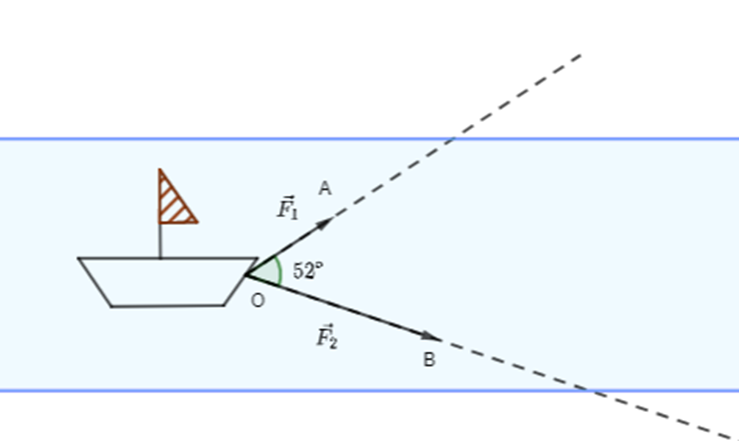
Độ lớn của vectơ hợp lực →F là tổng của hai lực →F1 và →F2 nằm trong khoảng nào dưới đây?
Hai người cùng kéo một con thuyền với hai lực →F1=→OA,→F2=→OB có độ lớn lần lượt là 550 N, 800 N. Cho biết góc giữa hai vectơ là 52o.

Độ lớn của vectơ hợp lực →F là tổng của hai lực →F1 và →F2 nằm trong khoảng nào dưới đây?
A. (900; 1 000);
A. (900; 1 000);
B. (1 000; 1 100);
B. (1 000; 1 100);
C. (1 100; 1 200);
C. (1 100; 1 200);
D. (1 200; 1 300).
D. (1 200; 1 300).
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là D
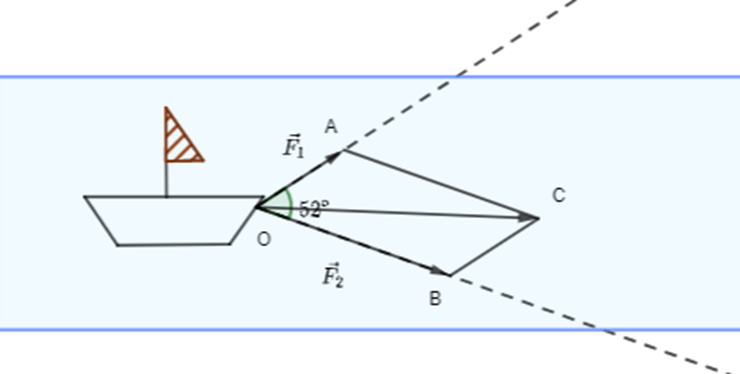
Dựng hình bình hành AOBC.
Khi đó →F=→OC.
Do AOBC là hình bình hành nên ^AOB+^OBC=180∘ và OA = BC = 550.
Do đó ^OBC=180∘−^AOB=180∘−52∘=128∘.
Áp dụng định lí côsin vào tam giác OBC có:
OC2 = OB2 + BC2 - 2.OB.BC.cos ^OBC
⇒ OC2 = 8002 + 5502 - 2.800.550.cos 128o
⇒ OC2 ≈ 1 484 282, 1
⇒ OC ≈ 1 218,3 N (do OC là độ dài đoạn thẳng nên OC > 0)
Suy ra |→F| ≈ 1 218,3 N.
Vậy độ lớn lực →F nằm trong khoảng (1 200; 1 300).
Đáp án đúng là D

Dựng hình bình hành AOBC.
Khi đó →F=→OC.
Do AOBC là hình bình hành nên ^AOB+^OBC=180∘ và OA = BC = 550.
Do đó ^OBC=180∘−^AOB=180∘−52∘=128∘.
Áp dụng định lí côsin vào tam giác OBC có:
OC2 = OB2 + BC2 - 2.OB.BC.cos ^OBC
⇒ OC2 = 8002 + 5502 - 2.800.550.cos 128o
⇒ OC2 ≈ 1 484 282, 1
⇒ OC ≈ 1 218,3 N (do OC là độ dài đoạn thẳng nên OC > 0)
Suy ra |→F| ≈ 1 218,3 N.
Vậy độ lớn lực →F nằm trong khoảng (1 200; 1 300).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Cho tam giác ABC có I là trung điểm cạnh AB và G là trọng tâm tam giác ABC. Đẳng thức nào sau đây sai:
Cho tam giác ABC có I là trung điểm cạnh AB và G là trọng tâm tam giác ABC. Đẳng thức nào sau đây sai:
Câu 3:
Hai lực →F1,→F2 cùng tác động lên một vật, cho |→F1|=7N,|→F2|=3N. Tính độ lớn của hợp lực →F1+→F2(biết góc giữa →F1,→F2 bằng 45°).
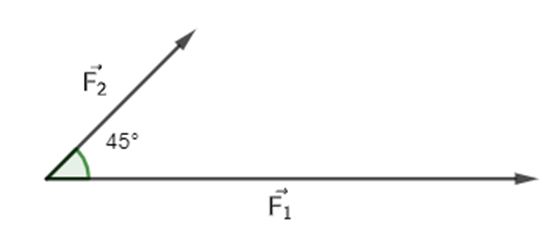
Hai lực →F1,→F2 cùng tác động lên một vật, cho |→F1|=7N,|→F2|=3N. Tính độ lớn của hợp lực →F1+→F2(biết góc giữa →F1,→F2 bằng 45°).

Câu 4:
Cho hình bình hành ABCD có tâm O, G là trọng tâm tam giác BCD. Đẳng thức nào sau đây sai?
Cho hình bình hành ABCD có tâm O, G là trọng tâm tam giác BCD. Đẳng thức nào sau đây sai?
Câu 5:
Cho hình bình hành ABCD có một điểm O bất kì. Đẳng thức nào sau đây đúng?
Cho hình bình hành ABCD có một điểm O bất kì. Đẳng thức nào sau đây đúng?
Câu 9:
Cho lục giác đều ABCDEF và O là tâm. Có bao nhiêu đẳng thức dưới đây là đẳng thức đúng?
1. →OA+→OB+→OE=→0;
II. →BC+→FE=→AD;
III. →OA+→OB+→OE=→EB;
IV. →AB+→CD+→FE=→0.
Cho lục giác đều ABCDEF và O là tâm. Có bao nhiêu đẳng thức dưới đây là đẳng thức đúng?
1. →OA+→OB+→OE=→0;
II. →BC+→FE=→AD;
III. →OA+→OB+→OE=→EB;
IV. →AB+→CD+→FE=→0.
Câu 10:
Cho hình vuông ABCD có cạnh bằng 1. So sánh độ dài của hai vectơ sau:
→a=(→AC+→BD)+→CB;
→b=→AB+→AD+→BC+→DA.
Cho hình vuông ABCD có cạnh bằng 1. So sánh độ dài của hai vectơ sau:
→a=(→AC+→BD)+→CB;
→b=→AB+→AD+→BC+→DA.
Câu 11:
Cho tam giác ABC vuông cân tại A, đường cao AH và BC = 10cm. Tính độ dài vectơ →AB+→AC.
Cho tam giác ABC vuông cân tại A, đường cao AH và BC = 10cm. Tính độ dài vectơ →AB+→AC.
Câu 12:
Cho hình thoi ABCD có độ dài cạnh bằng 2 dm và ^BAD=100∘. Tính độ dài vectơ →DA+→DC.
Cho hình thoi ABCD có độ dài cạnh bằng 2 dm và ^BAD=100∘. Tính độ dài vectơ →DA+→DC.
Câu 13:
Cho hình bình hành ABCD tâm O. Ba điểm M, N, P thỏa mãn:
+) →MA+→MD+→MB=→0;
+) →ND+→NB+→NC=→0;
+) →PM+→PN=→0.
Nhận xét nào sau đây đúng về M, N, P.
Cho hình bình hành ABCD tâm O. Ba điểm M, N, P thỏa mãn:
+) →MA+→MD+→MB=→0;
+) →ND+→NB+→NC=→0;
+) →PM+→PN=→0.
Nhận xét nào sau đây đúng về M, N, P.
Câu 14:
Cho hình vuông ABCD có cạnh bằng a và ba điểm G, H, K thỏa mãn: →KA+→KC=→0; →GA+→GB+→GC=→0; →HA+→HD+→HC=→0. Tính độ dài các vectơ →GH.
Cho hình vuông ABCD có cạnh bằng a và ba điểm G, H, K thỏa mãn: →KA+→KC=→0; →GA+→GB+→GC=→0; →HA+→HD+→HC=→0. Tính độ dài các vectơ →GH.


