Giải phương trình sau: (cos 4x - 6sin^2 x + 2) / (2sinx - 1)

Đề bài: Giải phương trình sau: $\frac{cos4x-6{\sin }^{2}x+2}{2\sin x-1}$

Trả lời

Hướng dẫn giải:

$\frac{cos4x-6{\sin }^{2}x+2}{2\sin x-1}=0$

Điều kiện xác định:

2sinx – 1 ≠ 0

$\begin{array}{l}\iff \sin x\ne \frac{1}{2}\\ \iff \sin x\ne \sin \frac{\pi }{6}\\ \iff \left\{\begin{array}{l}x\ne \frac{\pi }{6}+k2\pi \\ x\ne \frac{5\pi }{6}+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)\end{array}$

$\begin{array}{l}\frac{cos4x-6{\sin }^{2}x+2}{2\sin x-1}=0\\ \Rightarrow \cos 4x-6{\sin }^{2}x+2=0\\ \Rightarrow 2{\cos }^{2}2x-1+3-6{\sin }^{2}x+2=0\\ \iff 2{\cos }^{2}2x-1+3\left(1-2{\sin }^{2}x\right)-1=0\\ \iff 2\cos 2x\left(cos2x+2\right)-\left(cos2x+2\right)=0\\ \iff \left(2\cos 2x-1\right)\left(\cos 2x+2\right)=0\end{array}$

$\begin{array}{l}\iff 2\cos 2x-1=0\left(cos2x+2\ge 1\right)\\ \iff cos2x=\frac{1}{2}\\ \iff 2x=\pm \frac{\pi }{3}+k2\pi \left(k\in \mathbb{Z}\right)\\ \iff x=\pm \frac{\pi }{6}+k\pi \left(k\in \mathbb{Z}\right)\left(1\right)\end{array}$

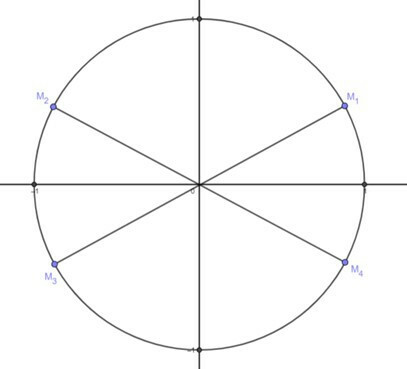
Họ nghiệm (1) biểu diễn bởi các điểm M₁, M₂, M₃, M₄ trên đường tròn lượng giác.

Họ nghiệm làm cho phương trình không xác định biểu diễn bởi các điểm M₁, M₂ trên đường tròn lượng giác.

Tổng hợp lại ta có nghiệm phương trình biểu diễn bởi các điểm M₃, M₄ trên đường tròn lượng giác.

Hay $x=\frac{-5\pi }{6}+k2\pi ;x=\frac{-\pi }{6}+k2\pi \left(k\in \mathbb{Z}\right)$