Giải phương trình: căn bậc ba (2 - c)^2 + căn bậc ba (7 + x)^2 - căn bậc ba
Giải phương trình: \[\sqrt[3]{{{{\left( {2 - x} \right)}^2}}} + \sqrt[3]{{{{\left( {7 + x} \right)}^2}}} - \sqrt[3]{{\left( {7 + x} \right)\left( {2 - x} \right)}} = 3\].
Đặt \(\sqrt[3]{{2 - x}} = a\) , \(\sqrt[3]{{7 + x}} = b\)
Suy ra a3 + b3 = 2 – x + 7 + x = 9
Ta có hệ phương trình
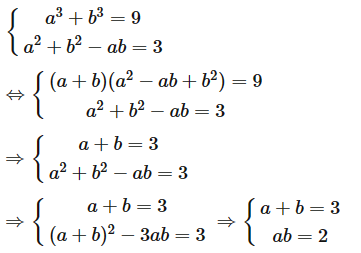
Theo định lý Vi – ét đảo thì a, b là nghiệm của phương trình X2 – 3X + 2 = 0
Do đó a = 1, b = 2 hoặc a = 2, b = 1.
+) Với a = 1, b = 2 ta có
• \(\sqrt[3]{{2 - x}} = 1\), suy ra x = 1 .
• \(\sqrt[3]{{7 + x}} = 2\), suy ra x = 1.
Do đó x = 1 thỏa mãn.
+) Với a = 2, b = 1 ta có
• \(\sqrt[3]{{2 - x}} = 2\), suy ra x = – 6
• \(\sqrt[3]{{7 + x}} = 1\), suy ra x = – 6
Do đó x = –6 thỏa mãn.
Vậy x = 1 hoặc x = – 6 .