Đồ thị hàm số y = ax^3 + bx^2 + cx + d có hai điểm cực trị là A(1; – 7) và B

Đề bài: Đồ thị hàm số y = ax³ + bx² + cx + d có hai điểm cực trị là A(1; – 7) và B (2;  – 8). Tính y(– 1)

A. y(– 1) = 7;

B. y(– 1) = 11;

C. y(– 1) = – 11;

D. y(– 1) = – 35.

Trả lời

Hướng dẫn giải:

Đáp án đúng là: D

Vì đồ thị hàm số đi qua A và B nên

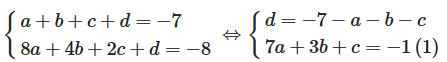
Ta có y’ = 3ax² + 2bx + c có hai nghiệm x = 1, x = 2 nên

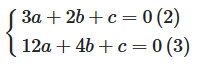
Từ (1), (2) và (3) suy ra

$$\begin{gathered} \left\{\begin{array}{l}7\text{a}+3b+c=-1\\ 3\text{a}+2b+c=0\\ 12\text{a}+4b+c=0\end{array}\right. \\ \iff \left\{\begin{array}{l}7\text{a}+3b+c=-1\\ \text{4a}+b=-1\\ \text{9a}+2b=0\end{array}\right. \\ \iff \left\{\begin{array}{l}a=2\\ b=-9\\ c=12\end{array}\right. \end{gathered}$$

Suy ra d = – 12

Khi đó y(– 1) = – a + b – c + d = – 35

Vậy ta chọn đáp án D.