Dãy số (un) cho bởi công thức số hạng tổng quát nào dưới đây là dãy số tăng

Bài 4 trang 105 Toán 11 Tập 2: Dãy số (u_n) cho bởi công thức số hạng tổng quát nào dưới đây là dãy số tăng?

A. $u_n=\frac{1}{n^2+1}$.

B. $u_n=2^{-n}$.

C. $u_n={\text{log}}_{\frac{1}{2}}n$.

D. $u_n=\frac{n}{n+1}$.

Trả lời

Đáp án đúng là: D

+) $u_n=\frac{1}{n^2+1}$.

Xét u_{n + 1} – u_n = 

, với mọi n $\in$ ℕ^*.

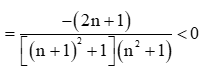
Do đó $u_n=\frac{1}{n^2+1}$là dãy số giảm.

+) $u_n=2^{-n}$. Ta có $u_n=2^{-n}>0,\forall n\in {\mathbb{N}}^{*}$.

Xét $\frac{u_{n+1}}{u_n}=\frac{2^{-(n+1)}}{2^{-n}}=2^{-(n+1)+n}=2^{-1}=\frac{1}{2}<1$.

Do đó $u_n=2^{-n}$ là dãy số giảm.

+) $u_n={\text{log}}_{\frac{1}{2}}n$.

Có a = $\frac{1}{2}$nên $u_n={\text{log}}_{\frac{1}{2}}n$luôn nghịch biến với n $\in$ ℕ^*.

Do đó $u_n={\text{log}}_{\frac{1}{2}}n$ là dãy số giảm.

+) $u_n=\frac{n}{n+1}$.

Xét u_{n + 1} – u_n = $\frac{n+1}{n+2}-\frac{n}{n+1}$ $=\frac{{\left(n+1\right)}^2-n\left(n+2\right)}{\left(n+2\right)\left(n+1\right)}$ $=\frac{1}{\left(n+2\right)\left(n+1\right)}>0$, với mọi n $\in$ ℕ^*.

Do đó$u_n=\frac{n}{n+1}$là dãy số tăng.

Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác: