Tìm các giá trị của tham số m để: a) Hàm số f(x)
Bài 26 trang 108 Toán 11 Tập 2: Tìm các giá trị của tham số m để:
a) Hàm số f(x) = 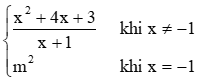
b) Hàm số g(x) = 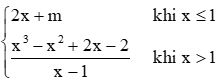
Bài 26 trang 108 Toán 11 Tập 2: Tìm các giá trị của tham số m để:
a) Hàm số f(x) = 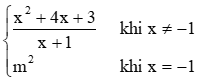
b) Hàm số g(x) = 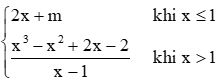
a) Ta có limx→−1f(x)=limx→−1x2+4x+3x+1=limx→−1(x+1)(x+3)x+1=limx→−1(x+3)=2 ; f(−1) = m2.
Để hàm số liên tục tại x = −1 thì limx→−1f(x)=f(−1) ⇔ m2 = 2 ⇔m=±√2 .
Vậy m=±√2 thì hàm số liên tục tại x = −1.
b) Ta có x < 1 thì g(x) = 2x + m liên tục với mọi x < 1.
Có x > 1 thì g(x) = x3−x2+2x−2x−1 liên tục với mọi x > 1.
Tại x = 1, ta có: limx→1−g(x)=limx→1−(2x+m)=2+m.
limx→1+g(x)=limx→1+x3−x2+2x−2x−1=limx→1+x2(x−1)+2(x−1)x−1
=limx→1+(x2+2)(x−1)x−1=limx→1+(x2+2)=3.
Có g(1) = 2 ∙ 1 + m = 2 + m.
Hàm số đã cho liên tục trên ℝ khi và chỉ khi hàm số liên tục tại x = 1
⇔limx→1−g(x)=limx→1+g(x)=g(1) ⇔ 2 + m = 3 ⇔ m = 1.
Vậy m = 1 thì hàm số đã cho liên tục trên ℝ.
Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác: