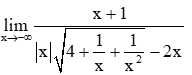Tính các giới hạn sau: a) lim từ n đến dương vô cùng của (1+3+5+...+(2n-1))/(n^2+2n+3
261
08/12/2023
Bài 25 trang 108 Toán 11 Tập 2: Tính các giới hạn sau:
a) limn→+∞1+3+5+⋯+(2n−1)n2+2n+3 ;
b) limn→+∞(1+23+49+⋯+2n3n) ;
c) limx→−22x2+3x−2x2−4 ;
d) limx→−∞(√4x2+x+1+2x) .
Trả lời
a) Ta có 1; 3; 5; …; 2n – 1 là một cấp số cộng có 2n−1−12+1=n (số hạng).
Suy ra 1 + 3 + 5 + … + (2n – 1) = 1+2n−12⋅n=n2 .
Khi đó limn→+∞1+3+5+⋯+(2n−1)n2+2n+3=limn→+∞n2n2+2n+3=limn→+∞11+2n+3n2=1 .
b) Ta có 1;23;49;...;2n3n là một cấp số nhân với u1 = 1 và q = 23.
Khi đó limn→+∞(1+23+49+⋯+2n3n)=limn→+∞1−(23)n+11−23
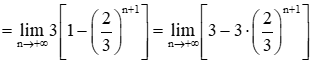 = 3.
= 3.
c) limx→−22x2+3x−2x2−4=limx→−2(2x−1)(x+2)(x−2)(x+2)=limx→−22x−1x−2=2⋅(−2)−1−2−2=54
d) limx→−∞(√4x2+x+1+2x)=limx→−∞x+1√4x2+x+1−2x= 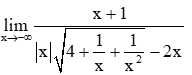
=limx→−∞x+1−x√4+1x+1x2−2x=limx→−∞1+1x−√4+1x+1x2−2=−14.
Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

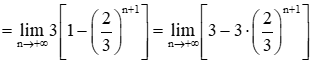 = 3.
= 3.