Giải các phương trình và bất phương trình sau: a) 3^1/x = 4
831
08/12/2023
Bài 27 trang 108 Toán 11 Tập 2: Giải các phương trình và bất phương trình sau:
a) 31x= 4;
b) 2x2−3x= 4;
c) log4 (x + 1) + log4 (x – 3) = 3;
d) (15)x2−2x≥1125 ;
e) (2−√3)x≤(2+√3)x+2 ;
f) log (3x2 + 1) > log (4x).
Trả lời
a) Điều kiện: x ≠ 0.
Ta có 31x=4⇔1x=log34⇔x=1log34=log43 (thỏa mãn).
Vậy nghiệm của phương trình là x = log43.
b) 2x2−3x=4⇔2x2−3x=22⇔x2−3x=2
⇔x2−3x−2=0⇔x=3+√172 hoặc x=3−√172 .
Vậy tập nghiệm của phương trình là S = 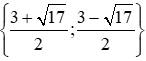 .
.
c) Điều kiện 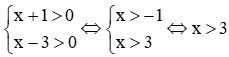 .
.
Ta có log4 (x + 1) + log4 (x – 3) = 3
⇔ log4 [(x + 1)(x – 3)] = 3
⇔ (x + 1)(x – 3) = 43
⇔ x2 – 2x – 67 = 0
⇔ x = 1 - 2√17 (loại) hoặc x = 1 + 2√17 (thỏa mãn).
Vậy nghiệm của phương trình là x = 1 + 2√17 .
d) Ta có (15)x2−2x≥1125⇔(15)x2−2x≥(15)3
⇔x2−2x≤3⇔x2−2x−3≤0⇔−1≤x≤3.
Vậy tập nghiệm của bất phương trình là S = [−1; 3].
e) (2−√3)x≤(2+√3)x+2
⇔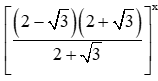 ≤(2+√3)x+2
≤(2+√3)x+2
⇔(12+√3)x≤(2+√3)x+2
⇔(2+√3)−x≤(2+√3)x+2.
Vậy tập nghiệm của bất phương trình là S = [−1; +∞).
f) Điều kiện: 4x > 0 ⇔ x > 0.
Ta có log (3x2 + 1) > log (4x) ⇔ 3x2 + 1 > 4x ⇔ 3x2 – 4x + 1 > 0 ⇔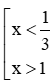 .
.
Kết hợp với điều kiện, ta có 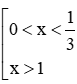 .
.
Vậy tập nghiệm của bất phương trình là S=(0;13)∪(1;+∞) .
Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

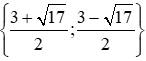 .
.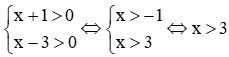 .
.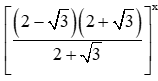
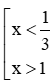 .
.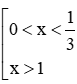 .
.