Có bao nhiêu giá trị nguyên của tham số m để hàm số $y=-x^4+6x^2+mx$ có ba điểm cực trị?

Chọn B

Ta có: $y\text{'}=-4x^3+12x+m$. Xét phương trình $y\text{'}=0\iff -4x^3+12x+m=0\left(1\right)$.

Để hàm số có ba điểm cực trị thì phương trình (1) phải có 3 nghiệm phân biệt.

Ta có: $\left(1\right)\iff m=4x^3-12x$.

Xét hàm số $g\left(x\right)=4x^3-12x$ có $g\text{'}\left(x\right)=12x^2-12$. Cho $g\text{'}\left(x\right)=0\iff 12x^2-12=0\iff x=\pm 1$.

Bảng biến thiên của $g\left(x\right)$

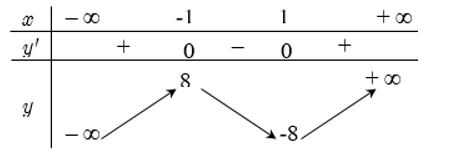
Dựa vào bảng biến thiên ta thấy, phương trình (1) có 3 nghiệm phân biệt khi $-8<m<8$.

Do $m\in \mathbb{Z}\Rightarrow m\in \left\{-7,-6,-5,\mathrm{...},5,6,7\right\}$.

Vậy có 15 giá trị nguyên của tham số m thỏa yêu cầu đề bài.